7.6: Probability

Probability measures the chance that an event occurs. Outcomes of dice rolling, card selection, and basketball shots are examples of discrete probabilities because they have a finite number of possible outcomes. In calculus we work with continuous probabilities, in which a number can take on any value. A store might want to determine the probability that a customer waits in line for more than \(2\) minutes, or a doctor might want to know the probability that her patient has a blood pressure above \(130 \un{mm Hg}.\) We discuss the following topics:

• Probability Density Functions
• Exponential Probability Density Functions
• Mean of a Probability Density Function
• Normal Distribution

Probability Density Functions

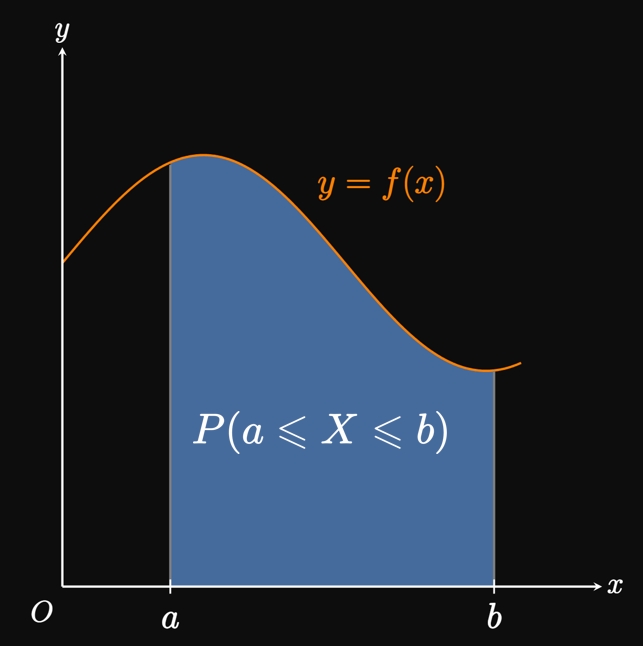
Let \(X\) denote a continuous random variable, meaning \(X\) is randomly assigned any number. The probability that the value of \(X\) lands between the numbers \(a\) and \(b\) is written as \[P(a \leq X \leq b) \pd\] Suppose that a continuous random variable \(X\) has a probability density function \(f,\) defined such that \(f(x) \geq 0\) and \begin{equation} P(a \leq X \leq b) = \int_a^b f(x) \di x \pd \label{eq:P-int} \end{equation} In words, to calculate the probability that \(X\) is between the numbers \(a\) and \(b,\) we find the area under the curve \(y = f(x)\) from \(x = a\) to \(x = b.\) (See Figure 1.) Because probabilities are measured from \(0\) to \(1,\) the total probability from \(x = -\infty\) to \(x = \infty\) must accumulate to \(1 \col\) \begin{equation} \int_{-\infty}^\infty f(x) \di x = 1 \pd \label{eq:prob-1} \end{equation} For a continuous random variable, we value probability density functions for the area under them; the particular values they output have little use to us.

Exponential Probability Density Functions

Exponential decay functions are excellent probability density functions for phenomena such as waiting times and equipment longevity. Consider the following examples: At the checkout counter, you'll likely be helped within a few minutes, whereas long wait times are rarer. Likewise, among people who call into a support center, few customers are willing to wait for a long time. And a light bulb is unlikely to function for much longer than its expected lifespan. To derive a general probability density function \(f\) for such models, we let \(t\) be time (in any unit) such that \(f(t) = 0\) for \(t \lt 0.\) (You cannot be helped before you enter the line.) We have, for \(k \gt 0,\) \[ f(t) = \bc 0 & t \lt 0 \nl Ce^{-kt} & t \geq 0 \pd \ec \] Let's derive an expression for the area under the curve \(y = f(t).\) Clearly, the area under \(f\) over \(t\) in \((-\infty, 0)\) is \(0.\) Thus, we evaluate the improper integral (using the methods of Section 6.5) as follows: \[ \ba \int_{-\infty}^\infty f(t) \di t &= \int_0^\infty Ce^{-kt} \di t \nl &= \lim_{b \to \infty} \int_0^b Ce^{-kt} \di t \nl &= \frac{C}{-k} \lim_{b \to \infty} \par{e^{-kt}} \intEval_0^b \nl &= \frac{C}{-k} \par{0 - 1} \nl &= \frac{C}{k} \pd \ea \] By \(\eqref{eq:prob-1},\) \(\int_{-\infty}^\infty f(t) \di t\) must equal \(1.\) So \(C/k = 1,\) meaning \(C = k.\) Accordingly, all exponential decay functions are of the form \begin{equation} f(t) = \bc 0 & t \lt 0 \nl ke^{-kt} & t \geq 0 \pd \ec \label{eq:exp-density} \end{equation} (See Figure 2.) If \(C \ne k,\) then \(\eqref{eq:prob-1}\) is not satisfied and so \(f(t)\) cannot be a probability density function.

Mean of a Probability Density Function

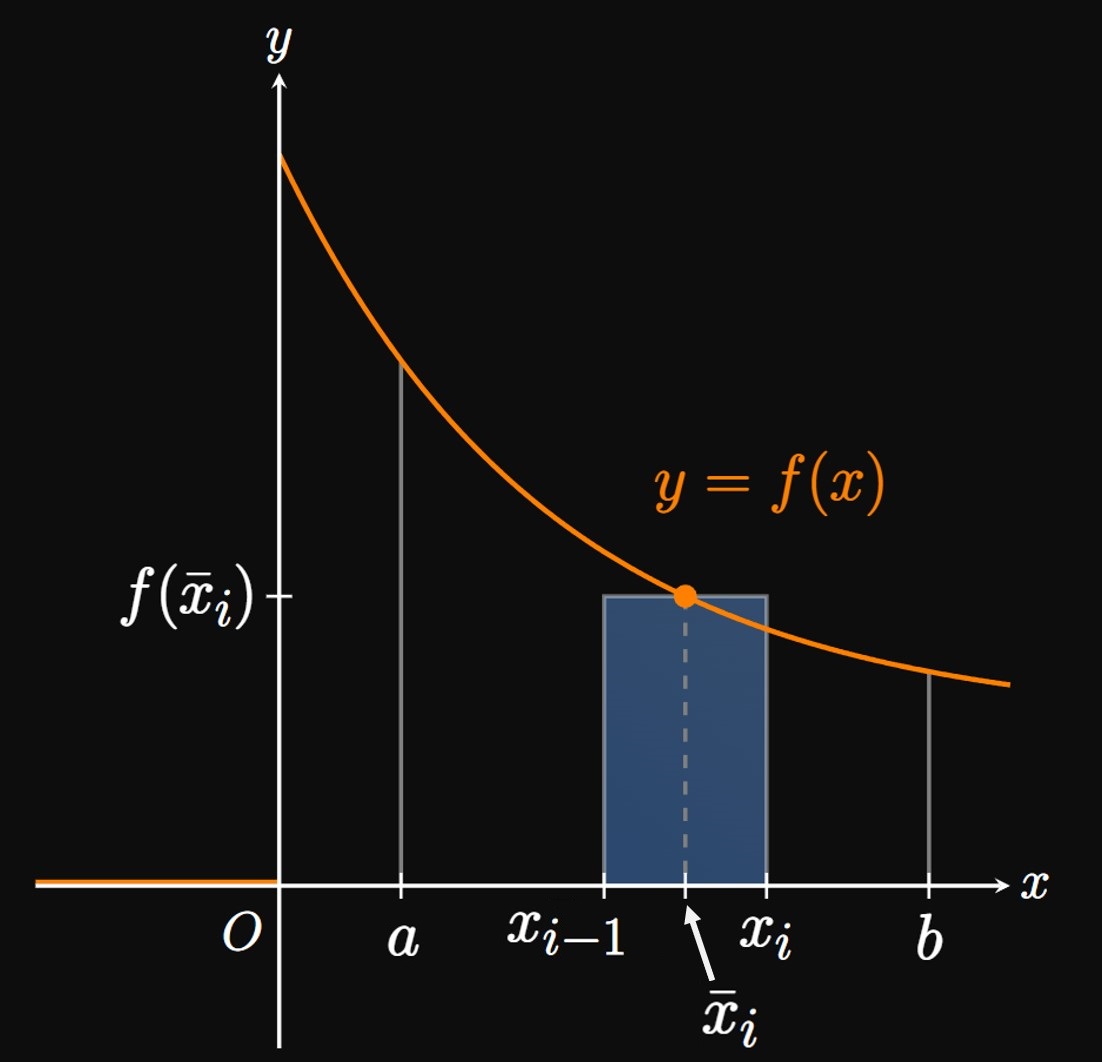
In a store or call center, it's imperative to know the average time a customer waits. Similarly, an equipment manufacturer must know how long a piece of equipment tends to last. These applications motivate the calculation of the mean of a probability density function—the long-run average value of a random variable \(X.\) Let \(y = f(x)\) be a probability density function. Suppose that \(N\) numbers are chosen in the interval \([a, b];\) we want to determine the sum of these \(N\) numbers. We split the interval \([a, b]\) into \(n\) subintervals; consider one subinterval from \(x_{i - 1}\) to \(x_i.\) If \(\overline{x}_i\) is the midpoint of these two numbers, then we assert the following: As we pick more and more numbers between \(x_{i - 1}\) and \(x_i,\) then the average of these numbers will approach \(\overline{x}_i.\) The probability of picking a number in \([a, b]\) and having it land in \([x_{i - 1}, x_i]\) is approximately \(f \par{\overline{x}_i} \Delta x,\) which is the area of the approximating rectangle in Figure 3. Accordingly, we estimate that the number of values landing in \([x_{i - 1}, x_i]\) is \(N f \par{\overline{x}_i} \Delta x.\) Each value is approximately \(\overline{x}_i,\) so the sum of these numbers is roughly \[N \, \overline{x}_i f \par{\overline{x}_i} \Delta x \pd\] To get the sum of all \(N\) numbers (across all \(n\) subintervals), we add the sums of the numbers in all \(n\) subintervals: \[\sum_{i = 1}^n N \, \overline{x}_i f \par{\overline{x}_i} \Delta x \pd\] This form is a Riemann sum for \(x f(x).\) We make each subinterval infinitely small by letting \(n \to \infty\) and \(\Delta x \to 0,\) so the limiting value of this Riemann sum is \[\int_a^b N x f(x) \di x \pd\] This is the sum of all \(N\) numbers, so we divide by \(N\) to get the mean \(\mu\) (mu): \[\mu = \int_a^b x f(x) \di x \pd\] More generally, the mean of a probability density function \(f(x)\) is given by \begin{equation} \mu = \int_{-\infty}^\infty x f(x) \di x \pd \label{eq:avg-X} \end{equation} This formula asserts that if we choose many values of the continuous random variable \(X,\) then the long-run average of \(X\) will be \(\mu.\) Observe that because \(\eqref{eq:avg-X}\) contains an extra term \(x\) in the integrand, the integral does not measure a probability; do not confuse it with \(\eqref{eq:prob-1}.\)

Since the mean of an exponential probability density function is \(\mu = 1/k\) (from Example 3), we can rewrite the probability density function in \(\eqref{eq:exp-density}\) as \begin{equation} f(t) = \bc 0 & t \lt 0 \nl \dfrac{e^{-t/\mu}}{\mu} & t \geq 0 \pd \ec \label{eq:prob-density-mu} \end{equation} This form is useful if we know the average waiting time \(\mu.\)

Normal Distribution

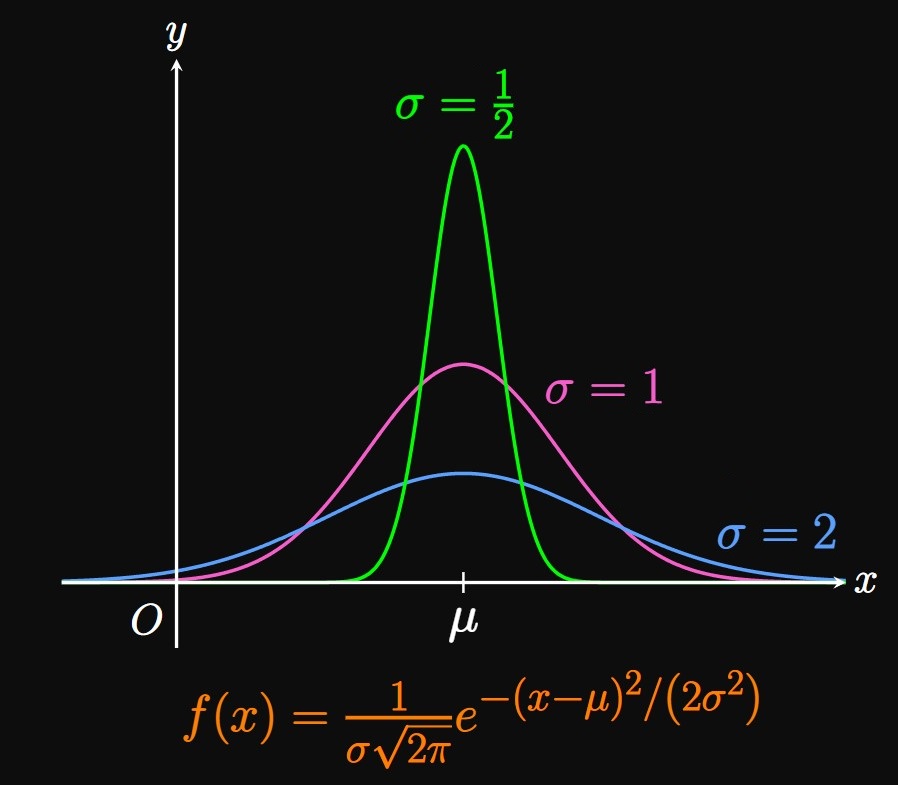
For centuries, statisticians have noticed a peculiar finding in homogeneous populations: Phenomena such as intelligence scores, test results, and heights are often distributed symmetrically around a central peak, resembling a bell curve. Specifically, a random variable \(X\) in these scenarios follows a Normal distribution, whose probability density function is \begin{equation} f(x) = \frac{1}{\sigma \sqrt{2 \pi}} \, e^{-(x - \mu)^2/\par{2 \sigma^2}} \pd \label{eq:normal-pdf} \end{equation} This is one of the most important distributions in statistics, with many applications in inferential statistics, probability calculations, and the natural sciences. It turns out that the factor \(1/\par{\sigma \sqrt{2 \pi}}\) is needed to satisfy \(\int_{-\infty}^\infty f(x) \di x = 1,\) thus enabling \(f\) to be a probability density function. The mean of this function is \(\mu,\) and the parameter \(\sigma\) (sigma) is called the standard deviation, a measure of variation in the values of \(X.\) Low values of \(\sigma\) imply little spread, meaning the graph of \(y = f(x)\) tends to be clustered around the mean. Conversely, high values of \(\sigma\) indicate large spread, so the graph of \(y = f(x)\) is more flattened around the mean. (See Figure 4.)

The 68–95–99.7 Rule Unfortunately, the function in \(\eqref{eq:normal-pdf}\) has no elementary antiderivative. We must instead use methods such as Riemann sums or Simpson's Rule to approximate integrals with this function. Using such methods produces the following results: \[ \ba \int_{\mu -\sigma}^{\mu + \sigma} \frac{1}{\sigma \sqrt{2 \pi}} \, e^{-(x - \mu)^2/\par{2 \sigma^2}} \di x &\approx 0.68 \cma\nl \int_{\mu -2\sigma}^{\mu + 2\sigma} \frac{1}{\sigma \sqrt{2 \pi}} \, e^{-(x - \mu)^2/\par{2 \sigma^2}} \di x &\approx 0.95 \cma \nl \int_{\mu -3\sigma}^{\mu + 3\sigma} \frac{1}{\sigma \sqrt{2 \pi}} \, e^{-(x - \mu)^2/\par{2 \sigma^2}} \di x &\approx 0.997 \pd \ea \] These results are summarized by the 68–95–99.7 Rule (also called the Empirical Rule), which says that about \(68\%\) of the data lie within \(1\) standard deviation of the mean, about \(95\%\) of the data lie within \(2\) standard deviations of the mean, and about \(99.7\%\) of the data lie within \(3\) standard deviations of the mean. Hence, it is very rare for a random variable \(X\) to lie more than \(3\) standard deviations away from the mean. We use the 68–95–99.7 Rule to estimate probabilities in our heads, as well as how likely an outcome is to occur. In general, statisticians consider significant any value of \(X\) located more than \(2\) standard deviations away from the mean, which has only a \(5\%\) chance to occur.

The Intelligence Quotient A measure of intelligence is the Intelligence Quotient (IQ), whose scores are Normally distributed with a mean of \(\mu = 100\) and a standard deviation of \(\sigma = 15.\) Substituting these parameters into \(\eqref{eq:normal-pdf}\) gives a probability density function for IQ scores to be \begin{equation} f(x) = \normalPdf{100}{15}{x} \pd \label{eq:iq} \end{equation} (See Figure 5.) By the 68–95–99.7 Rule, we conclude the following:

• About \(68 \%\) of people have IQs between \(85\) and \(115.\)
• About \(95 \%\) of people have IQs between \(70\) and \(130.\)
• About \(99.7 \%\) of people have IQs between \(55\) and \(145.\)

The heights of women in the United States are Normally distributed with an average height of \(64.5\) inches and a standard deviation of \(2.5\) inches (Figure 6).

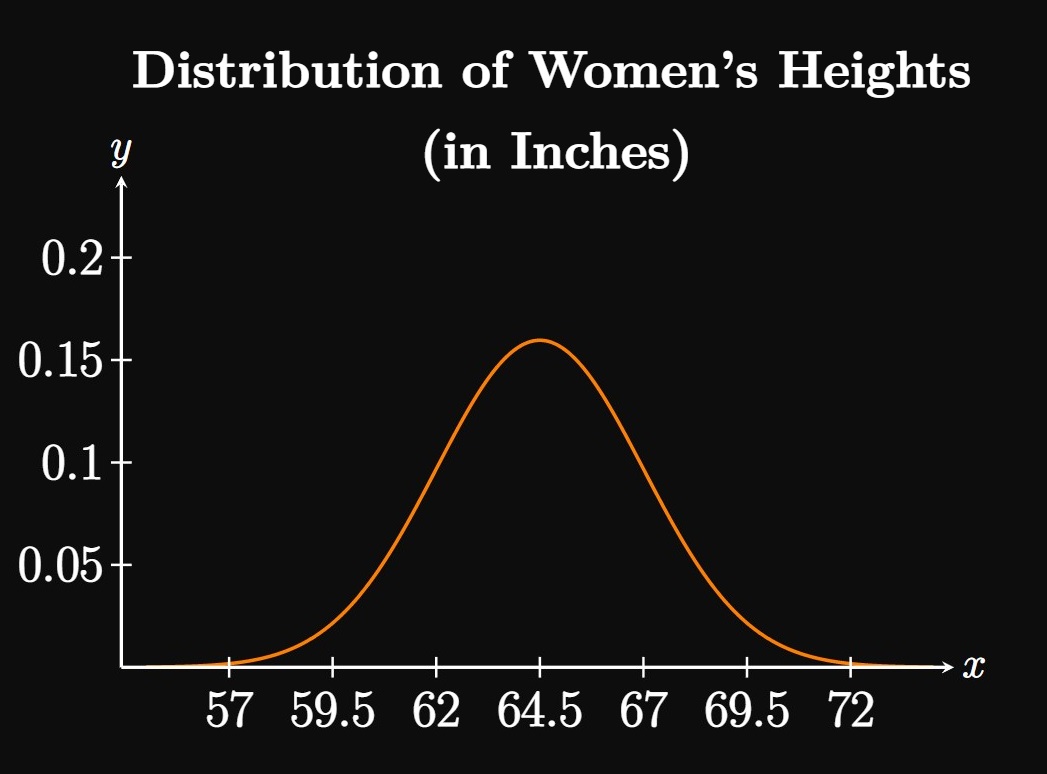
1. Derive the probability density function for this model.
2. In a sample of \(1000\) randomly selected women, approximately how many have a height between \(62\) inches and \(67\) inches?
3. What is the probability that a woman is \(68\) inches or taller?