2.9: Hyperbolic Functions
The exponential function has many applications; one such use involves defining special functions—hyperbolic functions, which have many analogies to trigonometric functions. In this section we discuss the following topics:
Defining Hyperbolic Functions
The hyperbolic sine and hyperbolic cosine functions are defined as follows: \begin{align} \sinh x &= \frac{e^x - e^{-x}}{2} \cma \label{eq:sinh} \nl \cosh x &= \frac{e^x + e^{-x}}{2} \pd \label{eq:cosh} \end{align} It turns out that hyperbolic sine is odd since \(\sinh(-x) = -\sinh x\) and hyperbolic cosine is even because \(\cosh(-x) = \cosh x.\) Thus, \(\sinh\) is an odd combination of exponential functions and \(\cosh\) is an even combination of exponential functions. The remaining four hyperbolic functions, similar to trigonometric functions, are named hyperbolic tangent, hyperbolic secant, hyperbolic cosecant, and hyperbolic cotangent. The following table summarizes the definitions of the six hyperbolic functions.
| \(\ds \sinh x = \frac{e^x - e^{-x}}{2}\) | \(\ds \cosh x = \frac{e^x + e^{-x}}{2}\) |
| \(\ds \tanh x = \frac{\sinh x}{\cosh x}\) | \(\ds \coth x = \frac{\cosh x}{\sinh x}\) |
| \(\ds \sech x = \frac{1}{\cosh x}\) | \(\ds \csch x = \frac{1}{\sinh x}\) |
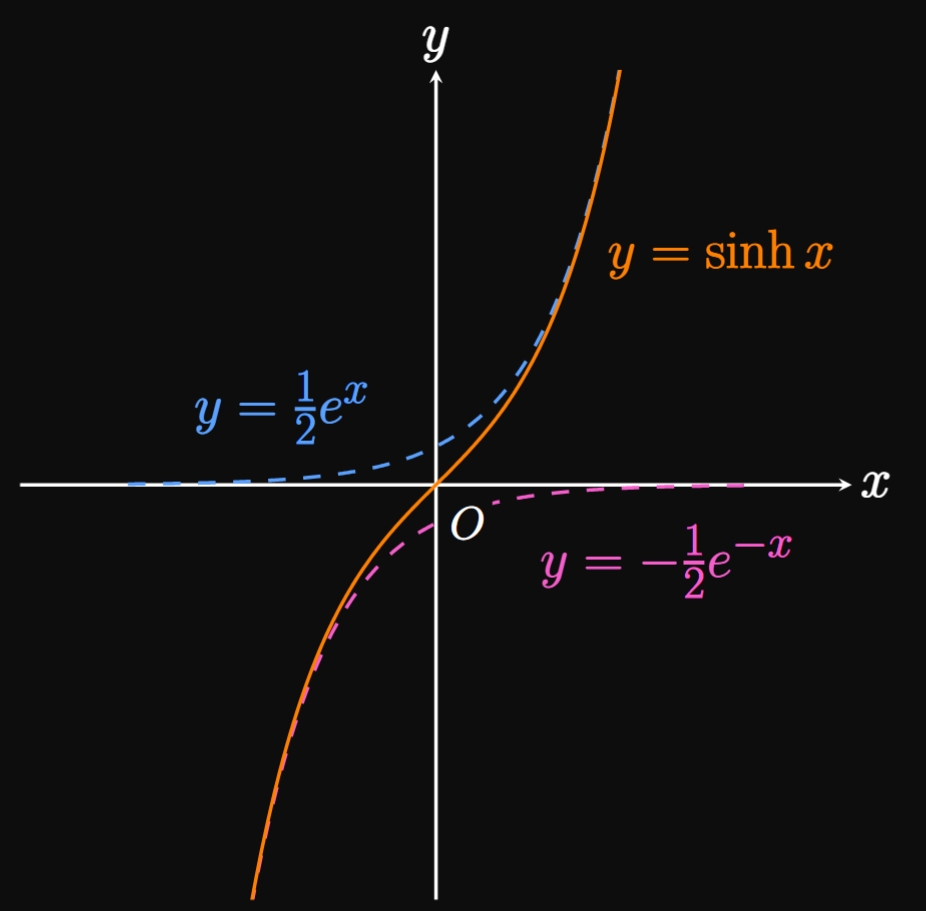
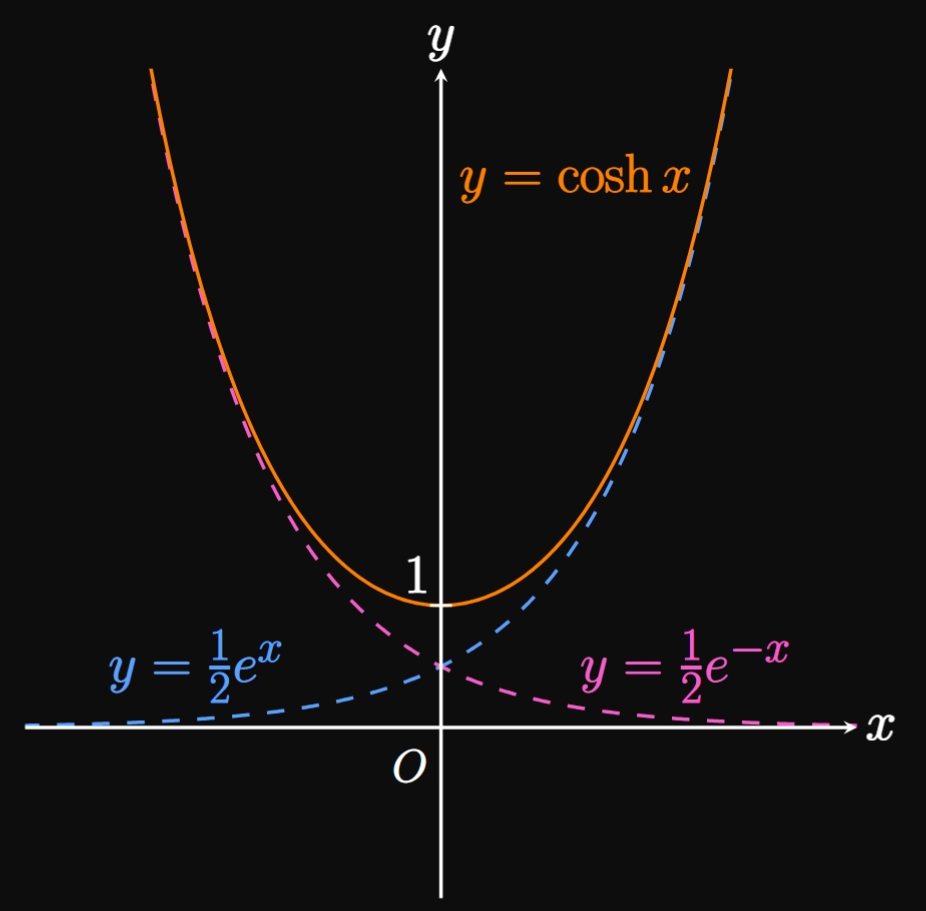
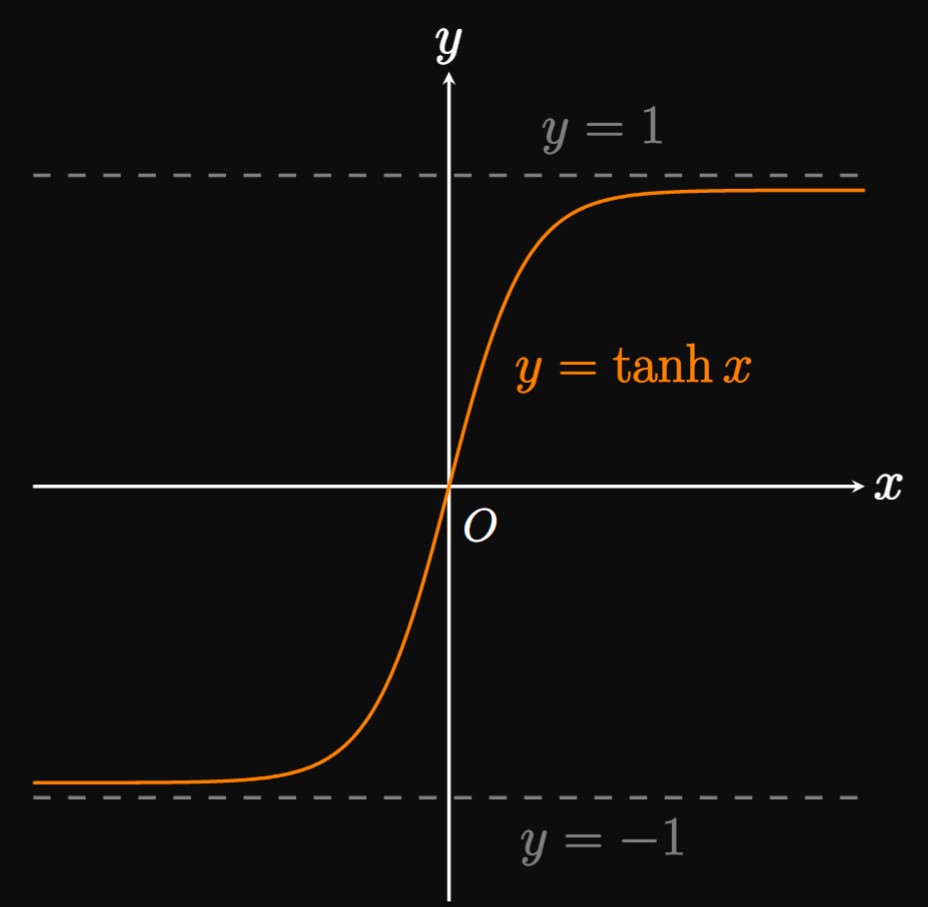
The graph of \(y = \sinh x\) can be sketched by summing the \(y\)-values of \(y = \frac{1}{2} e^{x}\) and \(y = -\frac{1}{2} e^{-x},\) as shown by Figure 1A. A similar procedure gives the graph of \(y = \cosh x\) in Figure 1B. The function \(\sinh x\) has a domain of \(\RR\) and a range of \(\RR,\) whereas \(\cosh x\) has a domain of \(\RR\) and a range of \([1, \infty).\) By the relationship \(\tanh x = (\sinh x)/(\cosh x),\) the graph of \(\tanh\) can be attained by dividing \(y\)-values. Doing so yields the graph in Figure 2, which has horizontal asymptotes of \(y = -1\) and \(y = 1.\)
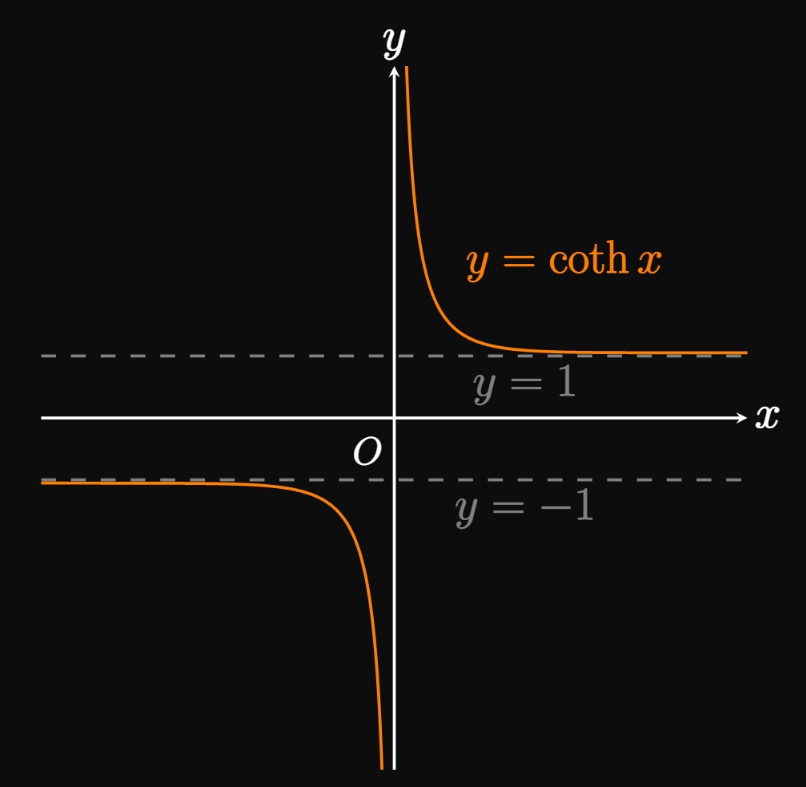
Similar reasoning gives the graphs of \(y = \csch x\) (Figure 3A), \(y = \sech x\) (Figure 3B), and \(y = \coth x\) (Figure 3C). The graphs of \(y = \csch x\) and \(y = \coth x\) each have a vertical asymptote at \(x = 0,\) whereas \(\sech x\) has a domain of \(\RR.\) The graphs of \(y = \csch x\) and \(y = \sech x\) each have a horizontal asymptote of \(y = 0,\) while the graph of \(y = \coth x\) has horizontal asymptotes of \(y = -1\) and \(y = 1.\)
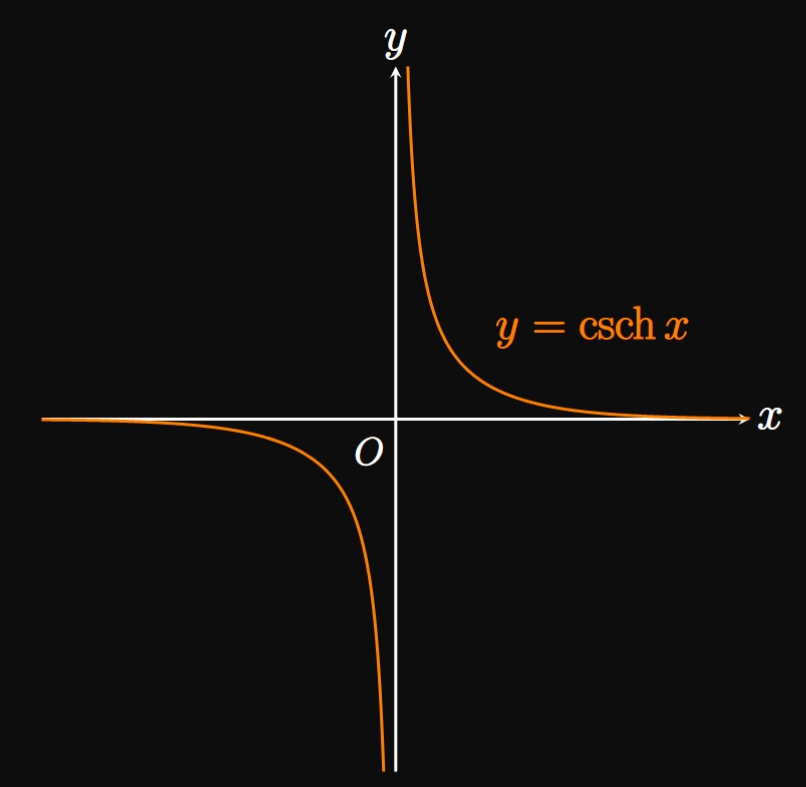

| Function | Domain | Range |
|---|---|---|
| \(\sinh x\) | \((-\infty, \infty)\) | \((-\infty, \infty)\) |
| \(\cosh x\) | \((-\infty, \infty)\) | \([1, \infty)\) |
| \(\tanh x\) | \((-\infty, \infty)\) | \((-1, 1)\) |
| \(\csch x\) | \((-\infty, 0) \cup (0, \infty)\) | \((-\infty, 0) \cup (0, \infty)\) |
| \(\sech x\) | \((-\infty, \infty)\) | \((0, 1]\) |
| \(\coth x\) | \((-\infty, 0) \cup (0, \infty)\) | \((-\infty, -1) \cup (1, \infty)\) |
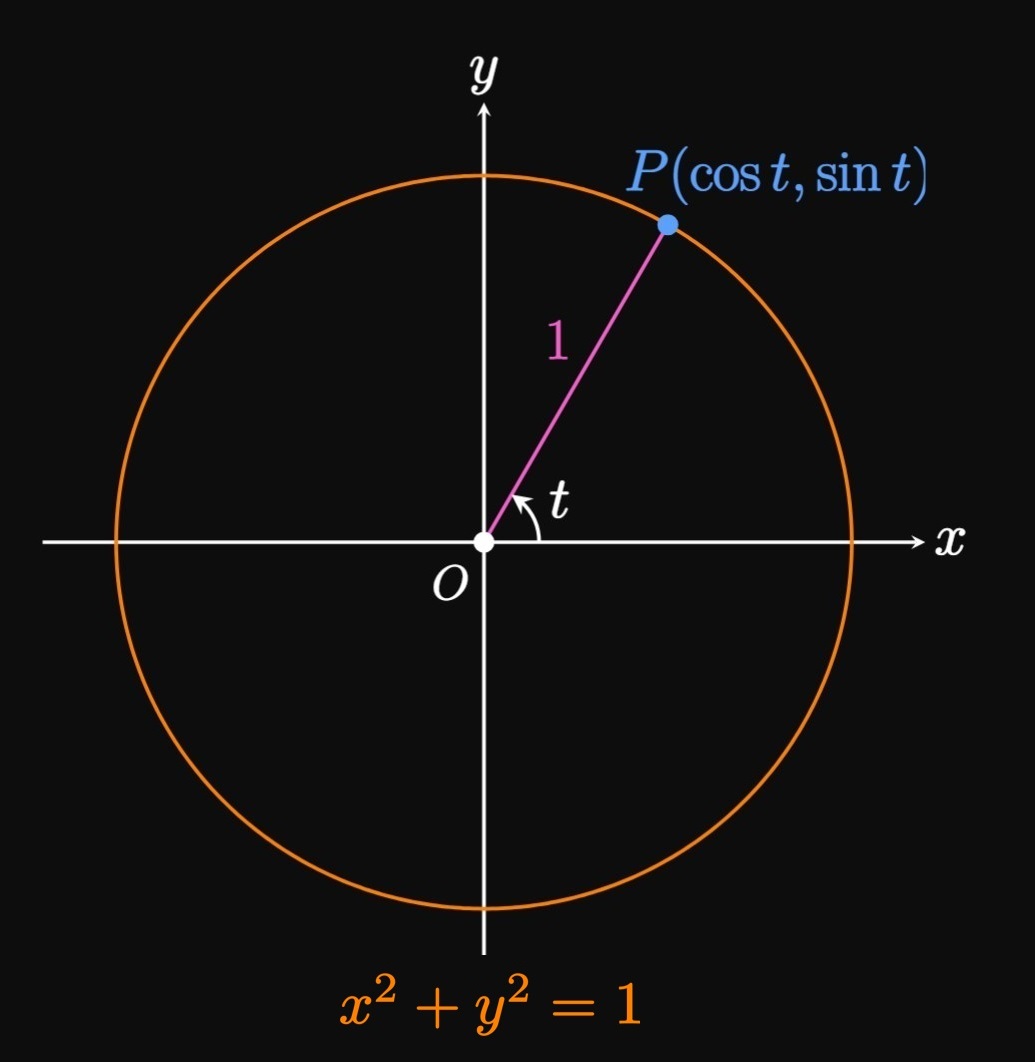
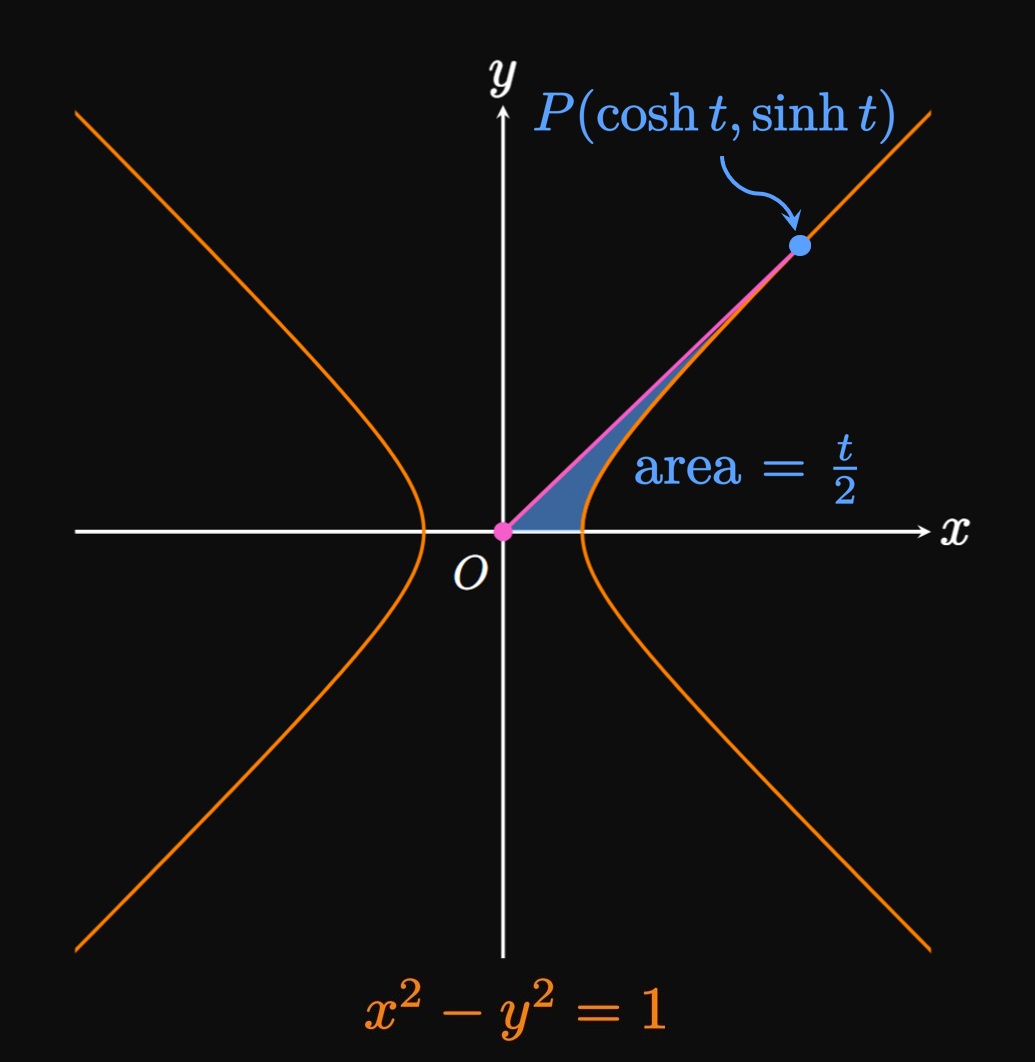
Geometric Interpretation If \(t\) is any real number, then the point \((\cos t, \sin t)\) is on the Unit Circle \(x^2 + y^2 = 1\) since \(\cos^2 t + \sin^2 t = 1.\) In this interpretation, \(t\) is the radian measure of the angle between the positive \(x\)-axis and segment \(\segment{OP}\) in Figure 4A. Why are hyperbolic functions given their name? Let's apply similar geometric reasoning: Consider the hyperbola \(x^2 - y^2 = 1.\) By analogy to the identity \(\cosh^2 t - \sinh^2 t\) \(= 1\) (the result of Example 1), we let \(x = \cosh t\) and \(y = \sinh t.\) Since \(\cosh t \geq 1,\) the point \(P(\cosh t, \sinh t)\) lies on the right branch of the hyperbola. Instead of \(t\) representing an angle, it happens to be double the area of the region bounded by the hyperbola's right branch, the \(x\)-axis, and segment \(\overline{OP}.\) (See Figure 4B.)
Hyperbolic identities are highly analogous to trigonometric identities. We list some identities below, whose proofs are left as exercises.
| \(\sinh(-x) = -\sinh x\) | \(\cosh(-x) = \cosh x\) |
| \(\cosh^2 x - \sinh^2 x = 1\) | \(\tanh^2 x + \sechPower{2} x = 1\) |
| \(\coth^2 x - \cschPower{2} x = 1\) | |
| \(\sinh(x + y) = \sinh x \cosh y + \cosh x \sinh y\) | |
| \(\cosh(x + y) = \cosh x \cosh y + \sinh x \sinh y\) |
Inverse Hyperbolic Functions
The graphs of \(y = \sinh x\) and \(y = \tanh x\) are one-to-one since they pass the Horizontal Line Test. We denote their inverse functions as \(\asinh x\) and \(\atanh x,\) respectively. Yet the graph of \(y = \cosh x\) only becomes one-to-one if we restrict its domain to \([0, \infty).\) The inverse of this restricted function is the inverse hyperbolic cosine function, \(\acosh x.\) The graphs of \(y = \asinh x,\) \(y = \acosh x,\) and \(y = \atanh x\) are shown in Figure 5A, Figure 5B, and Figure 5C, respectively. Likewise, the graphs of \(y = \csch x\) and \(y = \coth x\) are one-to-one, while the graph of \(y = \sech x\) becomes one-to-one if its domain is restricted to \([0, \infty).\) The same logic gives the graphs of \(y = \acsch x\) (Figure 5D), \(y = \asech x\) (Figure 5E), and \(y = \acoth x\) (Figure 5F).
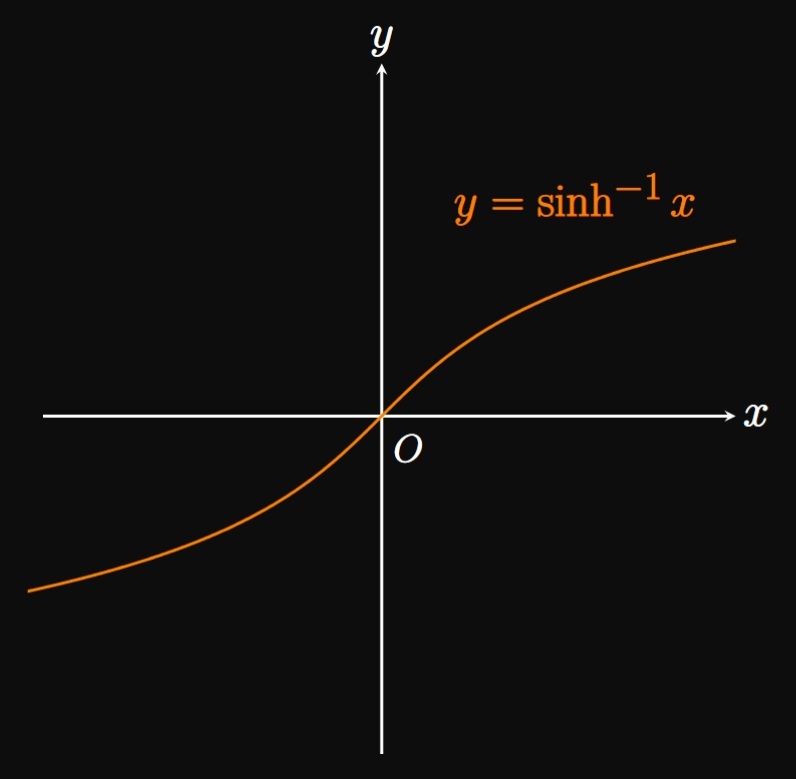

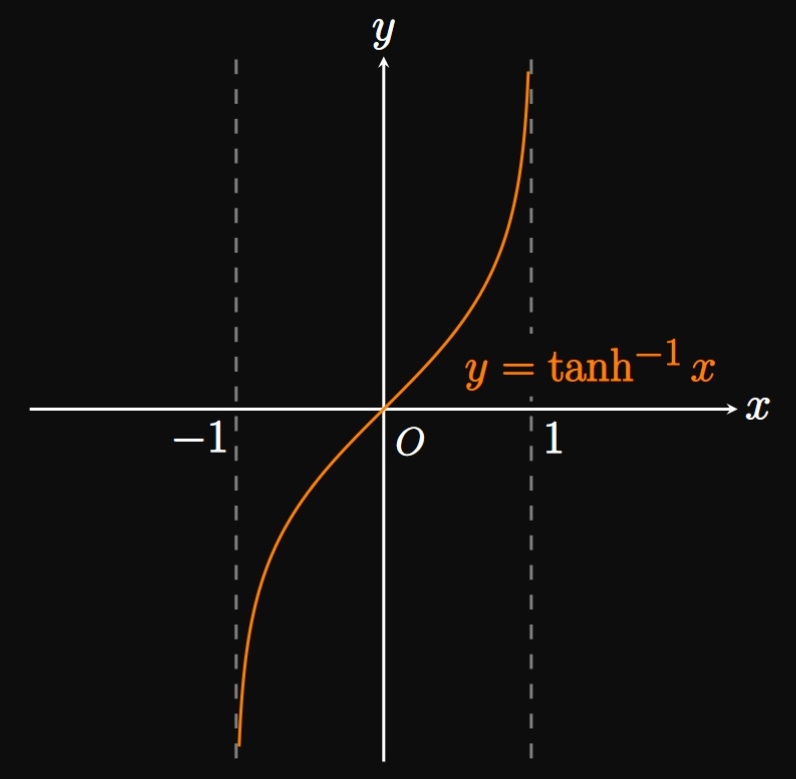
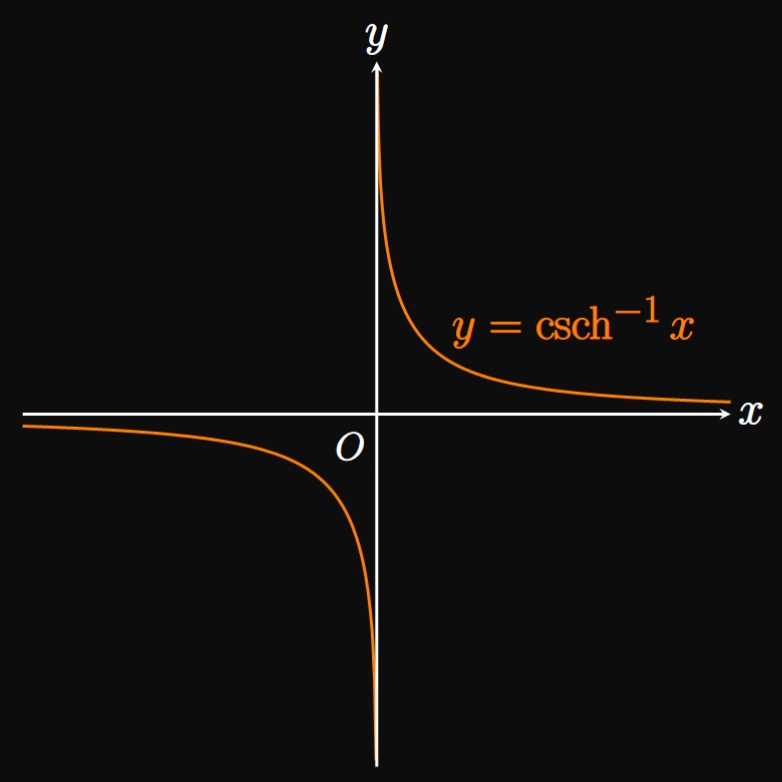
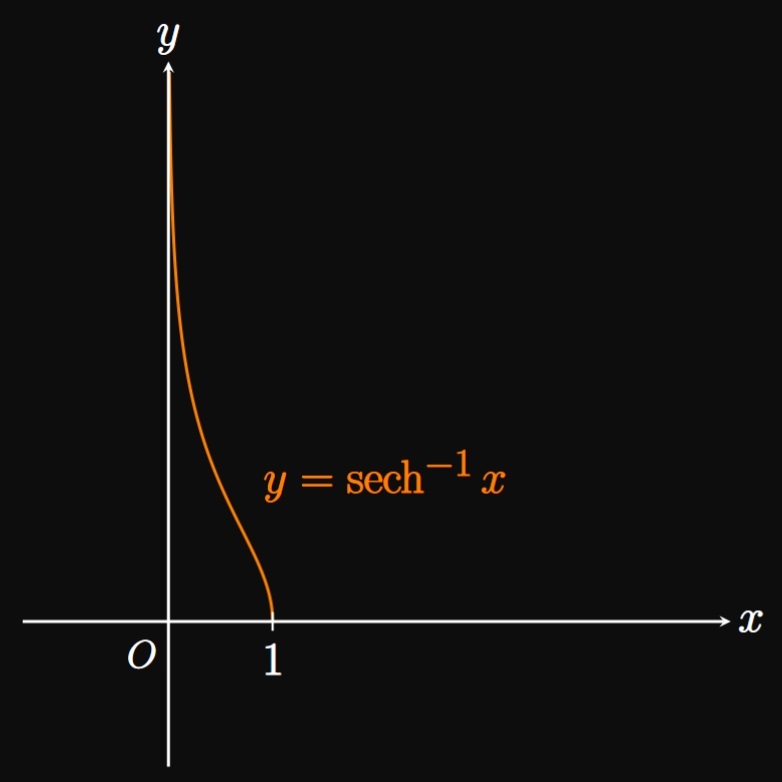
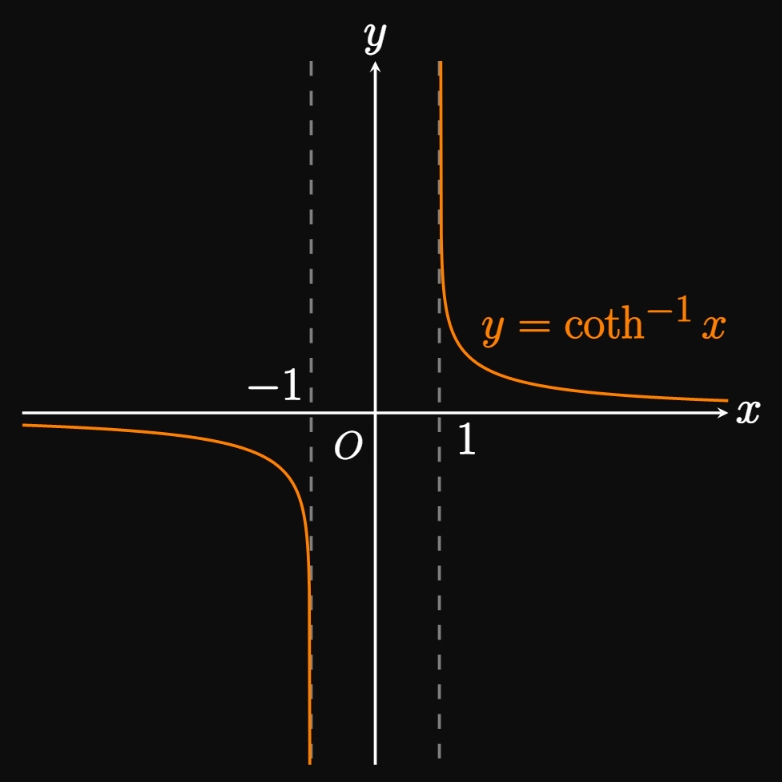
| Function | Domain | Range |
|---|---|---|
| \(\asinh x\) | \((-\infty, \infty)\) | \((-\infty, \infty)\) |
| \(\acosh x\) | \([1, \infty)\) | \([0, \infty)\) |
| \(\atanh x\) | \((-1, 1)\) | \((-\infty, \infty)\) |
| \(\acsch x\) | \((-\infty, 0) \cup (0, \infty)\) | \((-\infty, 0) \cup (0, \infty)\) |
| \(\asech x\) | \((0, 1]\) | \([0, \infty)\) |
| \(\acoth x\) | \((-\infty, -1) \cup (1, \infty)\) | \((-\infty, 0) \cup (0, \infty)\) |
Applying the same procedure of Example 2 enables us to express the other inverse hyperbolic functions in terms of the natural logarithm. Because hyperbolic functions are defined in terms of the exponential function, it's intuitive that inverse hyperbolic functions can be expressed in terms of the natural logarithm. The cases are listed in the following table.
| Identity | Domain |
|---|---|
| \(\ds \asinh x = \ln \par{x + \sqrt{x^2 + 1}}\) | \((-\infty, \infty)\) |
| \(\ds \acosh x = \ln \par{x + \sqrt{x^2 - 1}}\) | \([1, \infty)\) |
| \(\ds \atanh x = \tfrac{1}{2} \ln \par{\frac{1 + x}{1 - x}}\) | \((-1, 1)\) |
| \(\ds \acsch x = \ln \par{\frac{1}{x} + \frac{\sqrt{1 + x^2}}{\abs x}}\) | \((-\infty, 0) \cup (0, \infty)\) |
| \(\ds \asech x = \ln \par{\frac{1 + \sqrt{1 - x^2}}{x}}\) | \((0, 1]\) |
| \(\ds \acoth x = \tfrac{1}{2} \ln \par{\frac{x + 1}{x - 1}}\) | \((-\infty, -1) \cup (1, \infty)\) |
Differentiating Hyperbolic Functions
It's easy to differentiate hyperbolic functions by using the definitions of \(\eqref{eq:sinh}\) and \(\eqref{eq:cosh}.\) For example, \[\deriv{}{x} (\sinh x) = \deriv{}{x} \par{\frac{e^x - e^{-x}}{2}} = \frac{e^x + e^{-x}}{2} = \cosh x \pd\] Applying a similar procedure yields the following derivatives, which show many similarities to the derivatives of trigonometric functions. (Beware of the signs in some derivatives, however.)
| \(\ds \deriv{}{x} \par{\sinh x} = \cosh x\) | \(\ds \deriv{}{x} \par{\cosh x} = \sinh x\) |
| \(\ds \deriv{}{x} \par{\tanh x} = \sechPower{2} x\) | \(\ds \deriv{}{x} \par{\coth x} = -\cschPower{2} x\) |
| \(\ds \deriv{}{x} \par{\sech x} = -\sech x \tanh x\) | \(\ds \deriv{}{x} \par{\csch x} = -\csch x \coth x\) |
The procedure in Example 5 can be applied to the other inverse hyperbolic functions. Doing so gives the following list of derivatives; the remaining proofs are left as exercises.
| \(\ds \deriv{}{x} \par{\asinh x} = \frac{1}{\sqrt{1 + x^2}}\) | \(\ds \deriv{}{x} \par{\acosh x} = \frac{1}{\sqrt{x^2 - 1}}\) |
| \(\ds \deriv{}{x} \par{\atanh x} = \frac{1}{1 - x^2}\) | \(\ds \deriv{}{x} \par{\acoth x} = \frac{1}{1 - x^2}\) |
| \(\ds \deriv{}{x} \par{\asech x} = -\frac{1}{x \sqrt{1 - x^2}}\) | \(\ds \deriv{}{x} \par{\acsch x} = -\frac{1}{\abs x \sqrt{1 + x^2}}\) |

Applications of Hyperbolic Functions The most famous application of hyperbolic functions is the catenary, the shape of a cable hanging freely under the influence of gravity. This shape is not a parabola! It turns out to be the curve \[ y = a \cosh \par{\frac{x}{a}} + c \] for constants \(a\) and \(c.\) (See Figure 6.) Hanging chains, power lines, and even spider webs all take the shape of a catenary curve, and many landmark buildings were modeled by catenaries. The hyperbolic tangent function arises in another application: the speed of an ocean wave whose wavelength is \(L\) and depth is \(d\) is given by \[v = \sqrt{\frac{gL}{2 \pi} \, \tanh \par{\frac{2 \pi d}{L}}} \cma\] where \(g\) is the acceleration due to gravity, \(9.8\) meters per second squared. (See Figure 7.)

Defining Hyperbolic Functions The hyperbolic sine function is an odd combination of the exponential function, whereas the hyperbolic cosine function is an even combination of the exponential function. These functions are defined as follows: \begin{align} \sinh x &= \frac{e^x - e^{-x}}{2} \cma \eqlabel{eq:sinh} \nl \cosh x &= \frac{e^x + e^{-x}}{2} \pd \eqlabel{eq:cosh} \end{align} The other four hyperbolic functions—hyperbolic tangent, hyperbolic secant, hyperbolic cosecant, and hyperbolic cotangent—are defined as follows.
| \(\ds \tanh x = \frac{\sinh x}{\cosh x}\) | \(\ds \coth x = \frac{\cosh x}{\sinh x}\) |
| \(\ds \sech x = \frac{1}{\cosh x}\) | \(\ds \csch x = \frac{1}{\sinh x}\) |
The following table lists the properties of each function.
| Function | Domain | Range |
|---|---|---|
| \(\sinh x\) | \((-\infty, \infty)\) | \((-\infty, \infty)\) |
| \(\cosh x\) | \((-\infty, \infty)\) | \([1, \infty)\) |
| \(\tanh x\) | \((-\infty, \infty)\) | \((-1, 1)\) |
| \(\csch x\) | \((-\infty, 0) \cup (0, \infty)\) | \((-\infty, 0) \cup (0, \infty)\) |
| \(\sech x\) | \((-\infty, \infty)\) | \((0, 1]\) |
| \(\coth x\) | \((-\infty, 0) \cup (0, \infty)\) | \((-\infty, -1) \cup (1, \infty)\) |
Hyperbolic functions satisfy identities that are analogous to those of trigonometric functions. Some identities are shown below.
| \(\sinh(-x) = -\sinh x\) | \(\cosh(-x) = \cosh x\) |
| \(\cosh^2 x - \sinh^2 x = 1\) | \(\tanh^2 x + \sechPower{2} x = 1\) |
| \(\coth^2 x - \cschPower{2} x = 1\) | |
| \(\sinh(x + y) = \sinh x \cosh y + \cosh x \sinh y\) | |
| \(\cosh(x + y) = \cosh x \cosh y + \sinh x \sinh y\) |
Inverse Hyperbolic Functions The graphs of all six hyperbolic functions except \(\cosh\) and \(\sech\) are one-to-one. By restricting the domains of \(\cosh\) and \(\sech,\) we attain the following six inverse hyperbolic functions.
| Function | Domain | Range |
|---|---|---|
| \(\asinh x\) | \((-\infty, \infty)\) | \((-\infty, \infty)\) |
| \(\acosh x\) | \([1, \infty)\) | \([0, \infty)\) |
| \(\atanh x\) | \((-1, 1)\) | \((-\infty, \infty)\) |
| \(\acsch x\) | \((-\infty, 0) \cup (0, \infty)\) | \((-\infty, 0) \cup (0, \infty)\) |
| \(\asech x\) | \((0, 1]\) | \([0, \infty)\) |
| \(\acoth x\) | \((-\infty, -1) \cup (1, \infty)\) | \((-\infty, 0) \cup (0, \infty)\) |
Inverse hyperbolic functions can be expressed in terms of the natural logarithm.
| Identity | Domain |
|---|---|
| \(\ds \asinh x = \ln \par{x + \sqrt{x^2 + 1}}\) | \((-\infty, \infty)\) |
| \(\ds \acosh x = \ln \par{x + \sqrt{x^2 - 1}}\) | \([1, \infty)\) |
| \(\ds \atanh x = \tfrac{1}{2} \ln \par{\frac{1 + x}{1 - x}}\) | \((-1, 1)\) |
| \(\ds \acsch x = \ln \par{\frac{1}{x} + \frac{\sqrt{1 + x^2}}{\abs x}}\) | \((-\infty, 0) \cup (0, \infty)\) |
| \(\ds \asech x = \ln \par{\frac{1 + \sqrt{1 - x^2}}{x}}\) | \((0, 1]\) |
| \(\ds \acoth x = \tfrac{1}{2} \ln \par{\frac{x + 1}{x - 1}}\) | \((-\infty, -1) \cup (1, \infty)\) |
Differentiating Hyperbolic Functions The derivative formulas for the hyperbolic functions are analogous to those for trigonometric functions, with a few differences in signs.
| \(\ds \deriv{}{x} \par{\sinh x} = \cosh x\) | \(\ds \deriv{}{x} \par{\cosh x} = \sinh x\) |
| \(\ds \deriv{}{x} \par{\tanh x} = \sechPower{2} x\) | \(\ds \deriv{}{x} \par{\coth x} = -\cschPower{2} x\) |
| \(\ds \deriv{}{x} \par{\sech x} = -\sech x \tanh x\) | \(\ds \deriv{}{x} \par{\csch x} = -\csch x \coth x\) |
The derivatives of the inverse hyperbolic functions are shown below.
| \(\ds \deriv{}{x} \par{\asinh x} = \frac{1}{\sqrt{1 + x^2}}\) | \(\ds \deriv{}{x} \par{\acosh x} = \frac{1}{\sqrt{x^2 - 1}}\) |
| \(\ds \deriv{}{x} \par{\atanh x} = \frac{1}{1 - x^2}\) | \(\ds \deriv{}{x} \par{\acoth x} = \frac{1}{1 - x^2}\) |
| \(\ds \deriv{}{x} \par{\asech x} = -\frac{1}{x \sqrt{1 - x^2}}\) | \(\ds \deriv{}{x} \par{\acsch x} = -\frac{1}{\abs x \sqrt{1 + x^2}}\) |
