Chapter 6: Integration Techniques
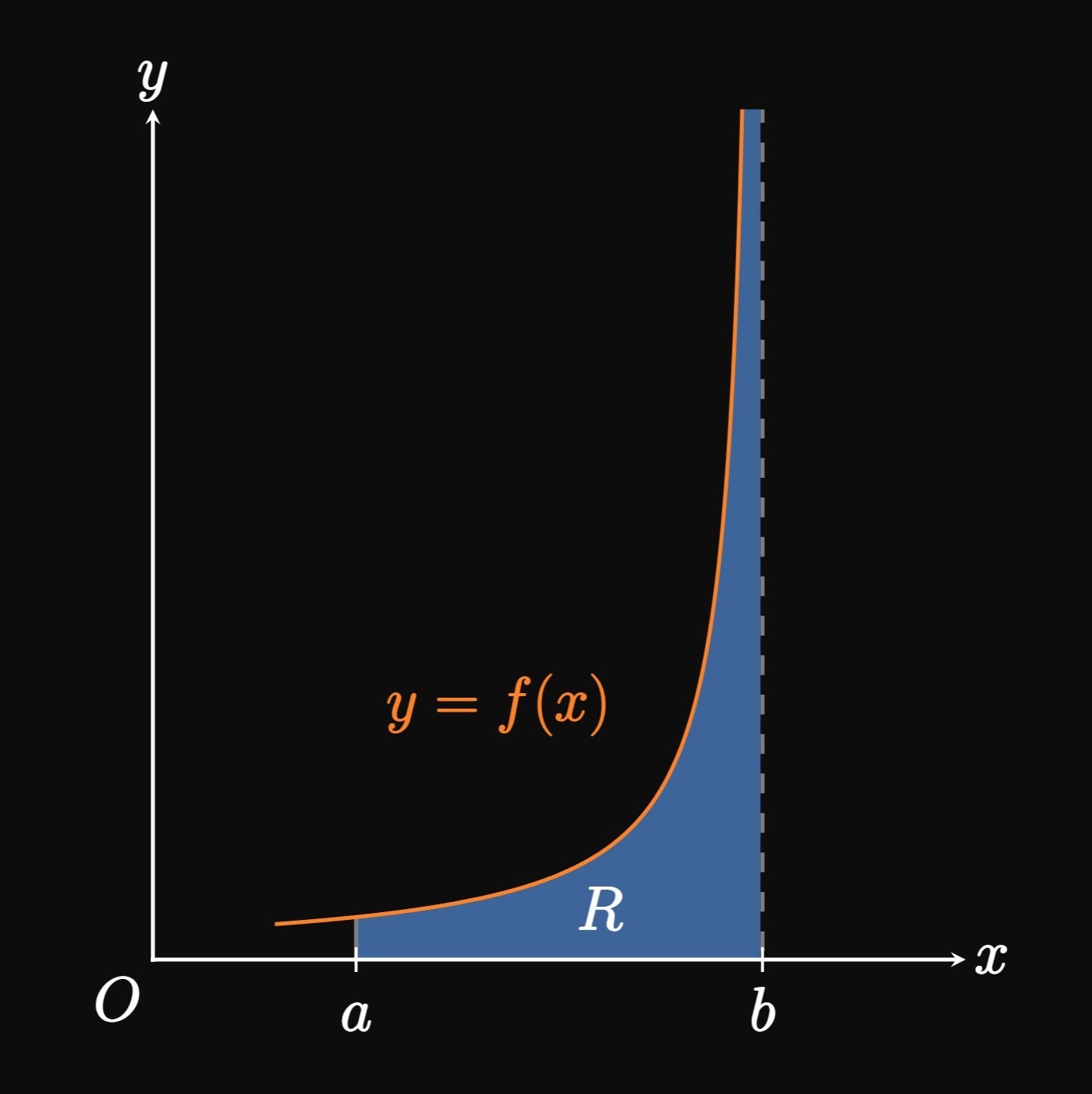
In Section 4.4 we learned the Substitution Rule, the most fundamental resource for integration. But integration isn't as straightforward as differentiation; there is no universal strategy. Instead, in this chapter we will study how to evaluate common types of integrals—integrals with products (6.1), trigonometric functions (6.2), radicals (6.3), and rational functions (6.4). We will also examine whether an unbounded region has an infinite area. The integral \(\int_{-1}^1 \dd x/x^2\) looks innocent, but in Section 6.5 you will understand why it diverges.
Sections
Derivation of Integration by Parts. Discussion of integrating products of functions.
Strategy for evaluating integrals with trigonometric functions using trigonometric identities and Integration by Parts. Integrals with sines and cosines, secants and tangents, and cosecants and cotangents. Integrals of products of sines and cosines.
6.3 Trigonometric Substitution
Transforming integrals with roots by using trigonometric substitutions. Discussion of cases of substitution and changing of bounds. Integration by reexpressing a rational expression as the sum of partial fractions. Discussion of partial fraction shapes: linear, reducible quadratic, irreducible quadratic, and higher-order irreducible polynomials. Integration of a function over an unbounded region (Type I improper integral) or through an infinite discontinuity (Type II improper integral). Discussing \(p\)-series. Comparison Tests for improper integrals.