5.6: Average Value of a Function

The average of a finite set of numbers is easy to compute, and it provides valuable information about the center of a dataset. But can the same utility be obtained for a continuous function? The average value of a function has a deep relationship with integration, and a special theorem connects the average value to a familiar geometric shape. We discuss these ideas through the following topics:

• Average Value of a Function
• Mean Value Theorem for Integrals

Average Value of a Function

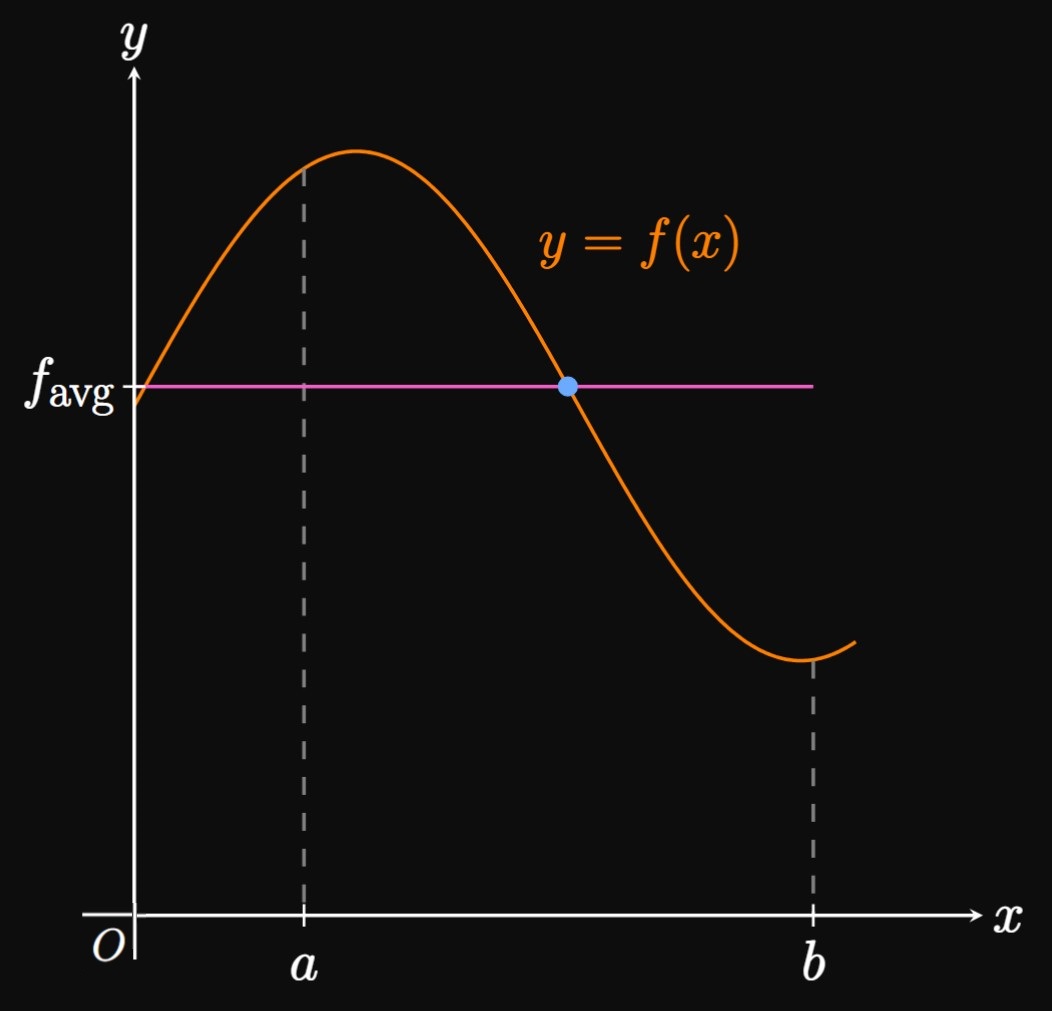
We know how to compute the average (arithmetic mean) of a finite set of numbers. The average of \(n\) numbers \(y_1, y_2, \dots, y_n\) is \[\avg{y} = \frac{y_1 + y_2 + \dots + y_n}{n} \pd \] But what if we wish to find the average of infinitely many numbers? Let's represent these numbers using the continuous function \(f\) over the interval \([a, b].\) To estimate the average value of \(f\) over \([a, b],\) we first cut the interval into \(n\) equal-width subintervals of endpoints \(a = x_0,\) \(x_1, \dots,\) \(x_{n - 1}, x_n.\) Note that each subinterval's width is \(\Delta x = (b - a)/n.\) Let \(x_1^*, x_2^*, \dots, x_n^*\) be sample points within each subinterval. The average value of \(f\) over \([a, b]\) is therefore approximated by \[\avg f \approx \frac{f(x_1^*) + f(x_2^*) + \cdots + f(x_n^*)}{n} \pd\] Since \(\Delta x = (b - a)/n,\) we have \(n = (b - a)/\Delta x.\) Thus, \[\avg f \approx \frac{f(x_1^*) + f(x_2^*) + \cdots + f(x_n^*)}{(b - a)/\Delta x} = \frac{1}{b - a} \parbr{f(x_1^*) + f(x_2^*) + \cdots + f(x_n^*)} \Delta x \pd\] As \(n\) increases, the subintervals shrink and so this expression better represents \(\avg f.\) If we let \(n \to \infty,\) then the approximation for \(\avg f\) improves in accuracy until it is exact. Hence, \[\avg f = \lim_{n \to \infty} \frac{1}{b - a} \parbr{f(x_1^*) + f(x_2^*) + \cdots + f(x_n^*)} \Delta x \pd\] The limit of the Riemann sum equals the expression \(1/(b - a) \int_a^b f(x) \di x,\) so \begin{equation} \avg f = \frac{1}{b - a} \int_a^b f(x) \di x \pd \label{eq:f-avg} \end{equation}

In Figure 1, \(\avg f\) is the average value of \(f\) over the interval \([a, b].\) If we view the curve as a two-dimensional mountain between \(x = a\) and \(x = b,\) then the following geometric property is true: Imagine cutting off the mountain's top and using it to fill in the mountain's bottom. The graph, for \(a \leq x \leq b,\) then becomes the uniform line \(y = \avg f.\)

Knowing the average value of a function is useful if measurements are taken continuously. For example, if the temperature of a city can be measured constantly (as opposed to every hour), then these measurements form a continuous function. You can bet that continuous temperature measurements are more accurate in determining the city's average temperature than are discrete hourly measurements.

From \(\eqref{eq:f-avg},\) the average value of \(f\) over \([0, 2]\) is \[ \ba \avg f &= \frac{1}{2 - 0} \int_0^2 (3x^2 + 1) \di x \nl &= \tfrac{1}{2} \par{x^3 + x} \intEval_0^2 \nl &= \tfrac{1}{2} (8 + 2) \nl &= \boxed 5 \ea \] (See Figure 2.)

Mean Value Theorem for Integrals

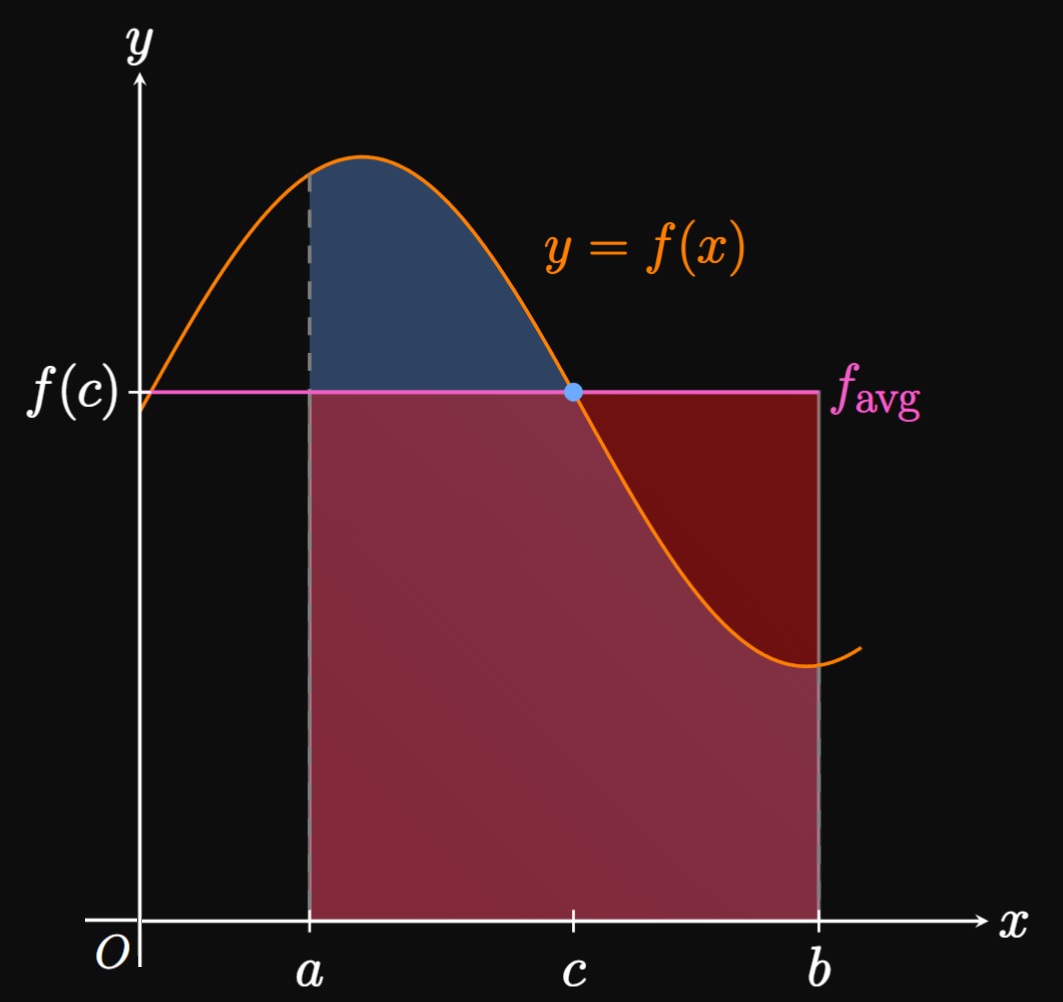
We know how to find the average of a continuous function \(f\) over the interval \([a, b].\) Now the question is whether \(f\) is guaranteed to take on this average value somewhere in this interval. The answer is yes! The Mean Value Theorem for Integrals guarantees a value \(c\) in this interval such that \(f(c) = \avg f.\)

Multiplying both sides of \(\eqrefer{eq:mvt-integrals}\) by \((b - a)\) gives \[\int_a^b f(x) \di x = f(c) (b - a) \pd\] This form asserts the following: Assume \(f\) is positive. In Figure 3, the rectangle of height \(f(c)\) and width \((b - a)\) equals the area of the region under \(f\) from \(a\) to \(b.\) For negative \(f,\) this same interpretation applies but with a negative rectangle area. Of course, multiple values of \(c\) can satisfy the Mean Value Theorem for Integrals for \(f\) over \([a, b].\)

PROOF This proof is based on the Mean Value Theorem we discussed in Section 3.2. Let \(F(x) = \int_a^x f(t) \di t\) for \(a \leq x \leq b.\) Since \(F\) is continuous over \([a, b]\) and differentiable over \((a, b),\) the Mean Value Theorem guarantees a value \(c\) in \((a, b)\) such that \[F'(c) = \frac{F(b) - F(a)}{b - a} = \frac{1}{b - a} \parbr{\int_a^b f(t) \di t - \int_a^a f(t) \di t} \pd\] Since \(\int_a^a f(t) \di t = 0,\) our expression simplifies to \[F'(c) = \frac{1}{b - a} \int_a^b f(t) \di t = \frac{1}{b - a} \int_a^b f(x) \di x \pd\] But by Part I of the Fundamental Theorem of Calculus, \(F'(c) = f(c).\) Hence, we have \[f(c) = \frac{1}{b - a} \int_a^b f(x) \di x = \avg f \pd\] \[\qedproof\]