3.5: Indeterminate Forms and L'Hopital's Rule

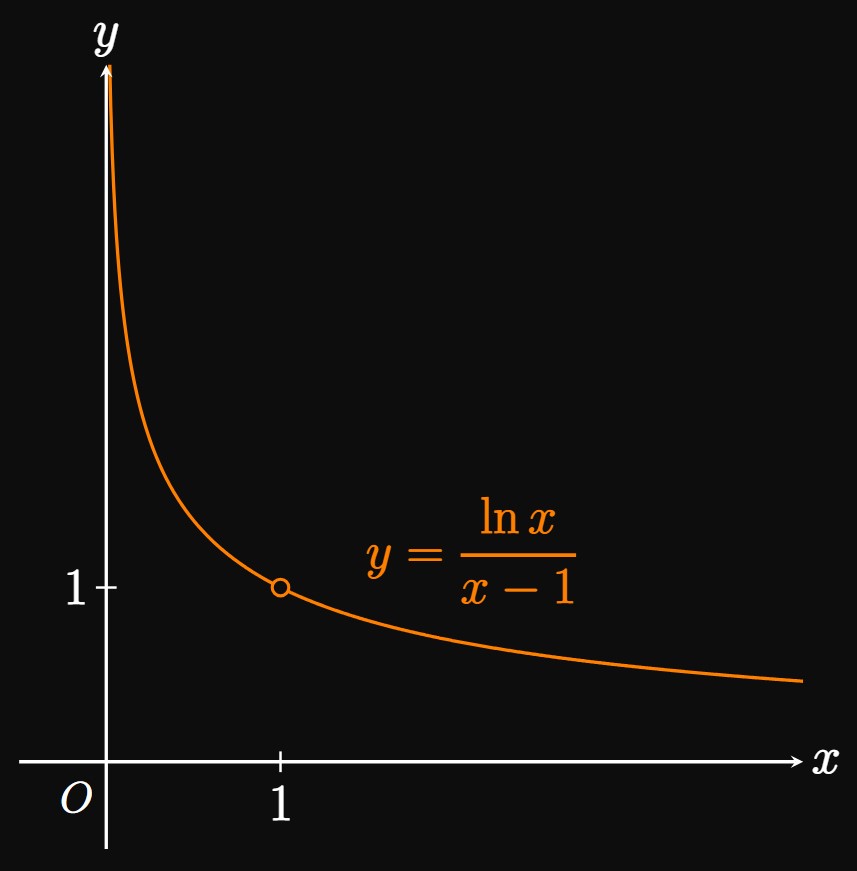
The functions \(\ln x\) and \((x - 1)\) both tend to \(0\) as \(x\) approaches \(1.\) Therefore, the limit is in the indeterminate form \(\indZero.\) Since these functions are differentiable, we apply L'Hôpital's Rule: \[ \ba \lim_{x \to 1}\frac{\ln x}{x - 1} &= \lim_{x \to 1} \frac{\deriv{}{x} (\ln x)}{\deriv{}{x} (x - 1)} \nl &= \lim_{x \to 1} \frac{1/x}{1} \nl &= \frac{1/1}{1} \nl &= \boxed{1} \ea \] As shown in Figure 1, the graph of \(y = (\ln x)/(x - 1)\) has a removable discontinuity at \((1, 1).\)

Because \(g\) is twice-differentiable, it follows that \(g\) and \(g'\) are both continuous (because differentiability requires continuity). We then have \[\lim_{x \to 0} [g(x) - \cos x] = g(0) - \cos 0 = 1 - 1 = 0 \pd\] In addition, \(\lim_{x \to 0} x^2 = 0,\) so the limit \[L = \lim_{x \to 0} \frac{g(x) - \cos x}{x^2}\] is in the indeterminate form \(\indZero.\) Therefore, we apply L'Hôpital's Rule: Differentiating the numerator and denominator gives \[L = \lim_{x \to 0} \frac{g'(x) + \sin x}{2x} \pd \] Since \(g'\) is continuous, \[\lim_{x \to 0} [g'(x) + \sin x] = g'(0) + \sin 0 = 0 + 0 = 0 \pd\] Likewise, \(\lim_{x \to 0} 2x = 0.\) Accordingly, the resulting limit is still in the indeterminate form \(\indZero.\) We use L'Hôpital's Rule again to get \[ \baat{2} L &= \lim_{x \to 0} \frac{g''(x) + \cos x}{2} \nl &= \frac{g''(0) + \cos 0}{2} &&\comment{g'' \text{ is continuous at } 0} \nl &= \frac{5 + 1}{2} \nl &= \boxed{3} \eaat \]

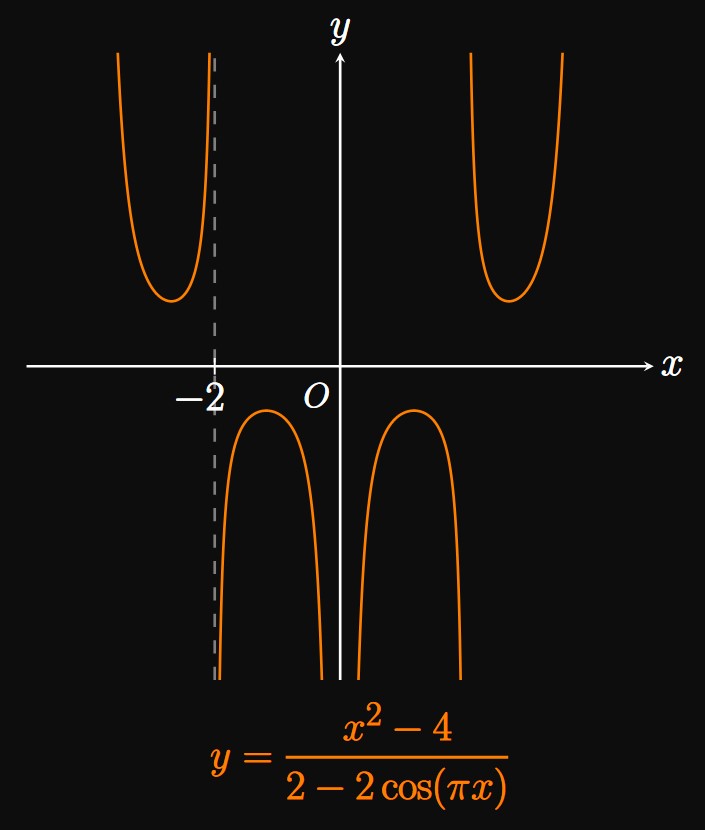
The numerator and denominator both approach \(0\) as \(x\) approaches \(-2,\) so the limit is in the indeterminate form \(\indZero.\) Both functions are differentiable, so we apply L'Hôpital's Rule: \[ \ba \lim_{x \to -2} \frac{x^2 - 4}{2 - 2 \cos(\pi x)} &= \lim_{x \to -2} \frac{\deriv{}{x}(x^2 - 4)}{\deriv{}{x}[2 - 2 \cos (\pi x)]} \nl &= \lim_{x \to -2} \frac{2x}{2 \pi \sin (\pi x)} \pd \nl \ea \] At \(x = -2,\) the denominator is \(0\) and the numerator is nonzero. Thus, the graph of \(y = 2x/[2 \pi \sin(\pi x)]\) has a vertical asymptote at \(x = -2.\) The limit therefore does not exist. (See Figure 2.)

We consider some ratio of \(f\) and \(g\) as \(x \to \infty\)—for example, \[L = \lim_{x \to \infty} \frac{f(x)}{g(x)} = \lim_{x \to \infty} \frac{x^{1/5}}{\ln x} \cma \] which is in the indeterminate form \(\indInfty.\) Therefore, we apply L'Hôpital's Rule to get \[ \ba L &= \lim_{x \to \infty} \frac{\frac{1}{5} x^{-4/5}}{1/x} \nl &= \lim_{x \to \infty} \frac{1}{5}x^{1/5} \nl &= \infty \pd \ea \] Because \(L = \infty,\) \(f(x) = x^{1/5}\) grows faster than \(g(x) = \ln x.\) As \(x\) approaches infinity, \(f(x)\) tries to force \(f(x)/g(x)\) to infinity, while \(g(x)\) tries to make the quotient decay to \(0.\) Because the quotient \(f(x)/g(x)\) approaches infinity, \(f(x) = x^{1/5}\) overpowers \(g(x) = \ln x\) and therefore grows faster.

REMARK This analysis shows that \(f(x) = x^{1/5}\) eventually grows faster than \(g(x) = \ln x.\) It turns out that \(x^{1/5}\) surpasses \(\ln x\) when \(x \approx 332\cmaNum105.108.\) An untrained observer may plot these functions and incorrectly conclude that \(g(x) = \ln x\) grows faster as \(x \to \infty.\)

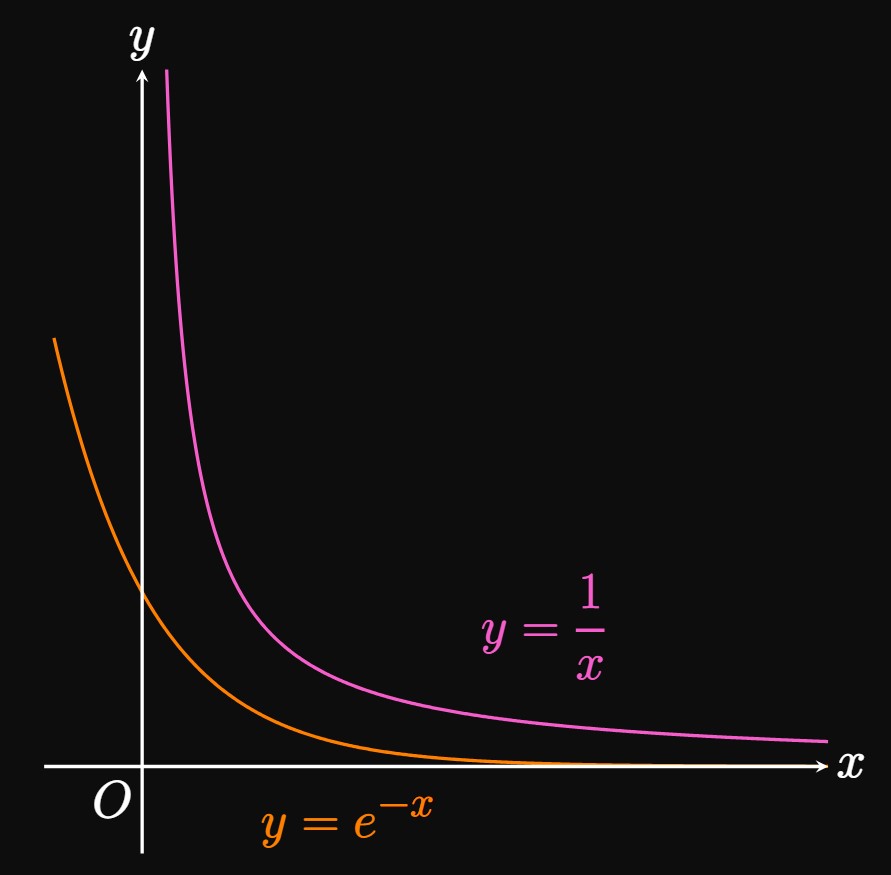
We consider some ratio of \(f\) and \(g\)—say, \[ \ba L &= \lim_{x \to \infty} \frac{f(x)}{g(x)} \nl &= \lim_{x \to \infty} \frac{e^{-x}}{1/x} \nl &= \lim_{x \to \infty} \frac{x}{e^x} \cma \ea \] which is in the indeterminate form \(\indInfty.\) Then applying L'Hôpital's Rule gives \[ \ba \lim_{x \to \infty} \frac{\deriv{}{x}(x)}{\deriv{}{x} \par{e^x}} &= \lim_{x \to \infty} \frac{1}{e^x} = 0 \pd \ea \] Since \(L = 0,\) we conclude that \(f(x) = e^{-x}\) decays faster than \(g(x) = 1/x.\) (See Figure 3.)

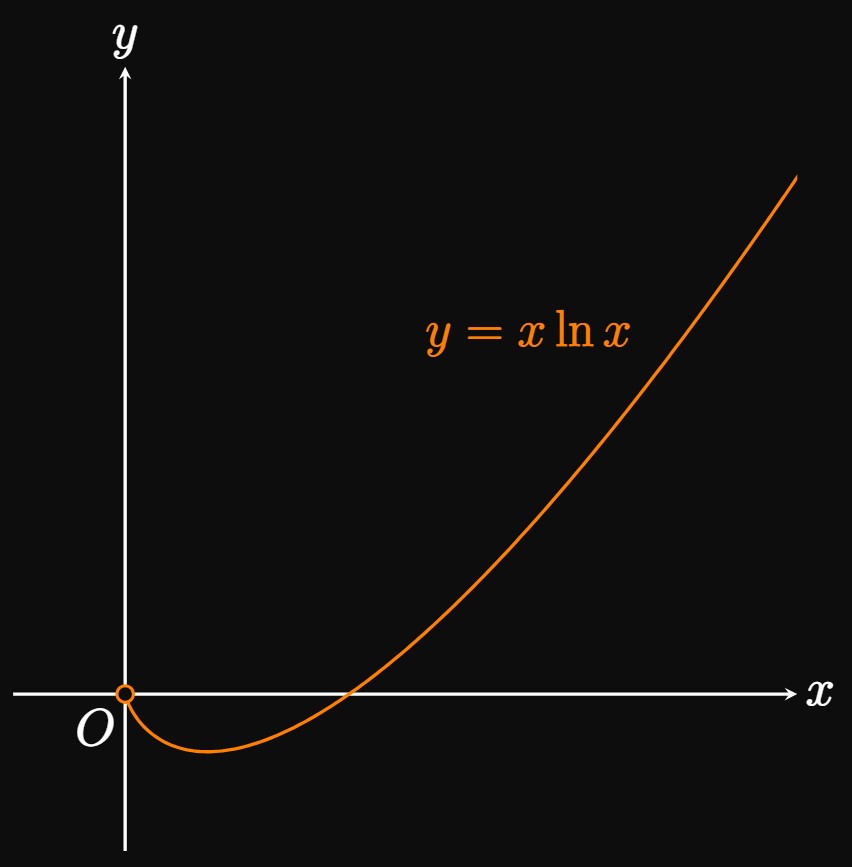
As \(x \to 0^+,\) \(x \to 0\) and \(\ln x \to -\infty.\) Thus, the limit \[L = \lim_{x \to 0^+} (x \ln x)\] is in the indeterminate form \(0 \times \infty.\) A battle exists between \(x\) and \(\ln x \col\) As \(x \to 0^+,\) the term \(x\) tries to force the product \(x \ln x\) to \(0,\) while \(\ln x\) tries to push the product to negative infinity. To analyze the limit, we rewrite the product \(x \ln x\) as some quotient—for example, \[L = \lim_{x \to 0^+} \frac{\ln x}{1/x} \cma \] which is in the indeterminate form \(\indInfty.\) By L'Hôpital's Rule, \[ \ba L &= \lim_{x \to 0^+} \frac{\deriv{}{x} (\ln x)}{\deriv{}{x} (1/x)} \nl &= \lim_{x \to 0^+} \frac{1/x}{-1/x^2} \nl &= \lim_{x \to 0^+} (-x) \nl &= \boxed{0} \ea \] Thus, as \(x \to 0^+,\) the term \(x\) overpowers \(\ln x\) and forces the product \(x \ln x\) to \(0.\) The graph of \(y = x \ln x\) is shown in Figure 4.

REMARK If we choose to rewrite the limit as \[L = \lim_{x \to 0^+} \frac{x}{1/(\ln x)} \cma\] then the limit is in the indeterminate form \(\indZero.\) Applying L'Hôpital's Rule would yield the same result, \(L = 0,\) through a slightly more cumbersome differentiation process.

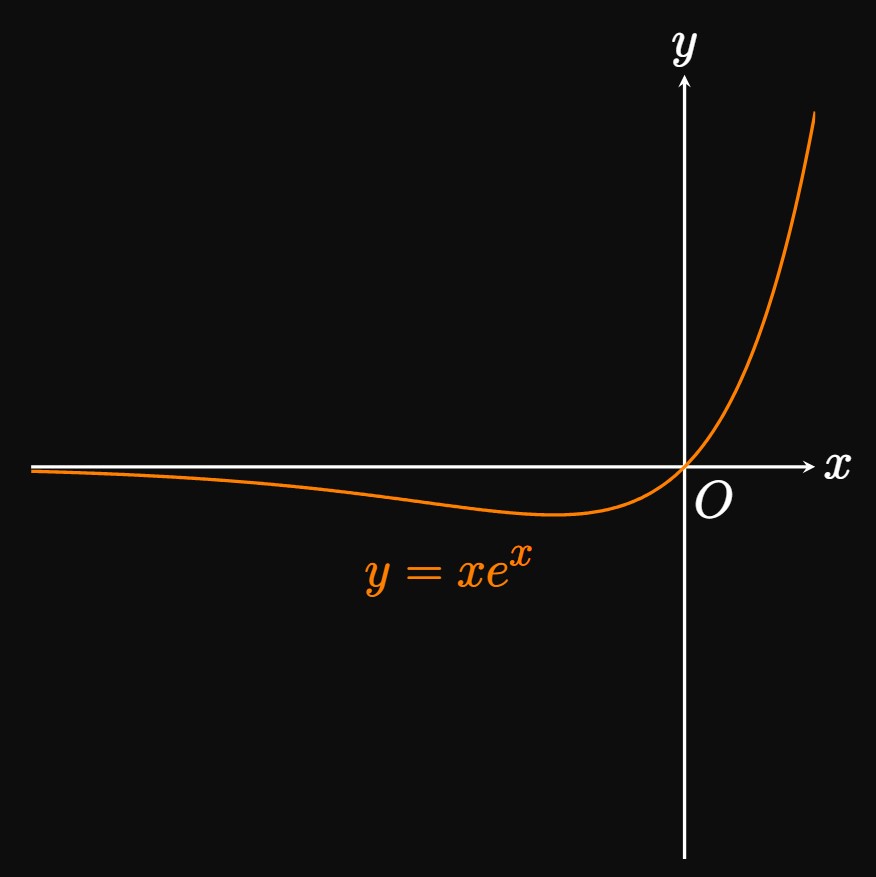
The limit is in the indeterminate form \(0 \times \infty,\) so we rewrite the expression as a quotient: \[ \lim_{x \to -\infty} xe^{x} = \lim_{x \to -\infty} \frac{x}{1/e^x} \cma \] which is in the indeterminate form \(\indInfty.\) Then by L'Hôpital's Rule, the limit is \[ \ba \lim_{x \to -\infty} \frac{\deriv{}{x}(x)}{\deriv{}{x} (1/e^x)} &= \lim_{x \to -\infty} \frac{1}{-1/e^x} \nl &= \lim_{x \to -\infty} -e^x \nl &= \boxed{0} \ea \] The graph of \(y = x e^x\) is shown in Figure 5.

A Bad Quotient If we choose the quotient \[\lim_{x \to -\infty} \frac{e^x}{1/x},\] which is in the indeterminate form \(\indZero,\) then L'Hôpital's Rule gives \[\lim_{x \to -\infty} \frac{e^x}{-1/x^2} \pd \] Further applications of L'Hôpital's Rule then give \[\lim_{x \to -\infty} \frac{e^x}{2/x^3} \cma \lim_{x \to -\infty} \frac{e^x}{-6/x^4} \cma \dots \cma\] leading nowhere because repeated iterations are still in the indeterminate form \(\indZero.\) In this problem only one choice, writing the quotient in the indeterminate form \(\indInfty,\) provides an answer.

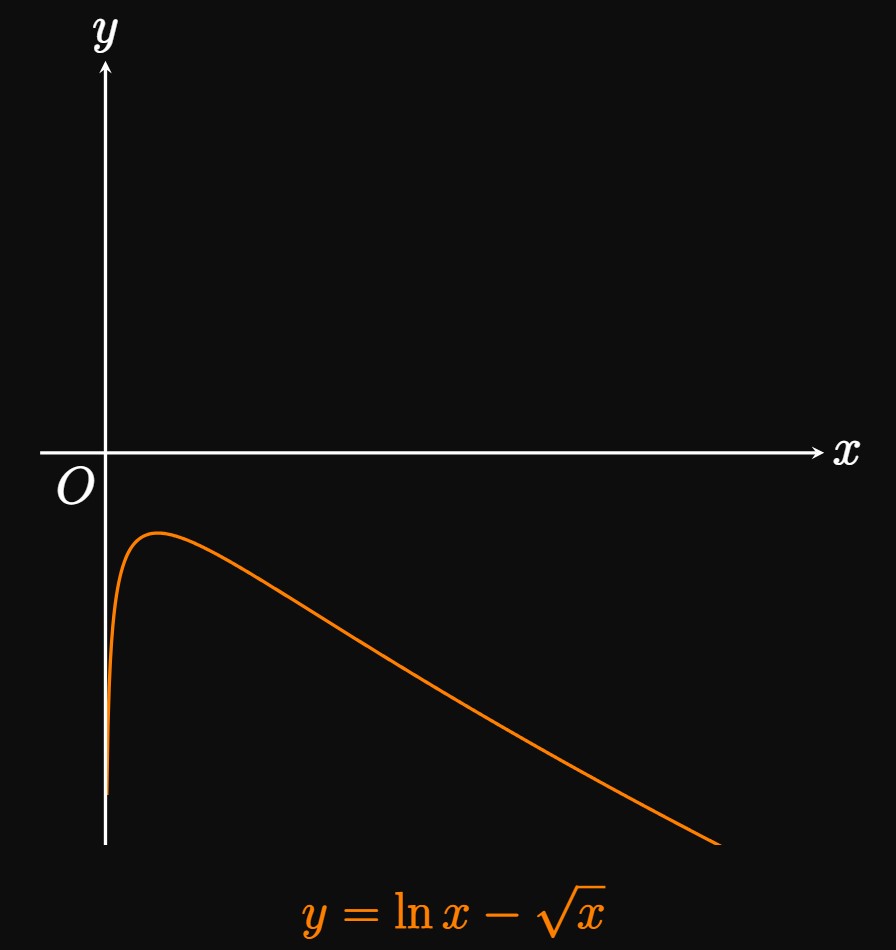
As \(x\) approaches infinity, both \(\ln x\) and \(\sqrt x\) approach infinity. Thus, the limit is in the indeterminate form \(\infty - \infty.\) Our goal is to manipulate the difference to be a product: Factoring out \(\sqrt x\) shows \[\lim_{x \to \infty} \par{\ln x - \sqrt x \,} = \lim_{x \to \infty} \sqrt x \left(\frac{\ln x}{\sqrt x} - 1 \right) \pd\] L'Hôpital's Rule gives \[ \ba \lim_{x \to \infty} \frac{\ln x}{\sqrt x} &= \lim_{x \to \infty} \frac{1/x}{\dfrac{1 \strut}{2 \sqrt x}} \nl &= \lim_{x \to \infty} \frac{2 \sqrt x}{x} \nl &= \lim_{x \to \infty} \frac{2}{\sqrt x} \nl &= 0 \pd \ea \] Thus, as \(x \to \infty,\) \[\left(\frac{\ln x}{\sqrt x} - 1 \right) \to -1 \pd\] Because \(\sqrt x \to \infty\) as \(x \to \infty,\) we must have \[\lim_{x \to \infty} \sqrt x \left(\frac{\ln x}{\sqrt x} - 1 \right) = \boxed{-\infty}\] The graph of \(y = \ln x - \sqrt x\) is shown in Figure 6.

REMARK If we choose to factor out \(\ln x,\) then the limit becomes \[\lim_{x \to \infty} \ln x \left(1 - \frac{\sqrt x}{\ln x} \right) \pd\] As \(x \to \infty,\) L'Hôpital's Rule shows \[ \ba \lim_{x \to \infty} \frac{\sqrt x}{\ln x} &= \lim_{x \to \infty} \frac{\dfrac{1 \strut}{2 \sqrt x}}{1/x} \nl &= \lim_{x \to \infty} \frac{x}{2 \sqrt x} \nl &= \lim_{x \to \infty} \frac{\sqrt x}{2} \nl &= \infty \pd \ea \] As \(x \to \infty,\) \[\ln x \to \infty \and \par{1 - \frac{\sqrt x}{\ln x}} \to - \infty \pd \] The product of \(\infty\) and \(-\infty\) is \(-\infty,\) so this approach yields the same answer.

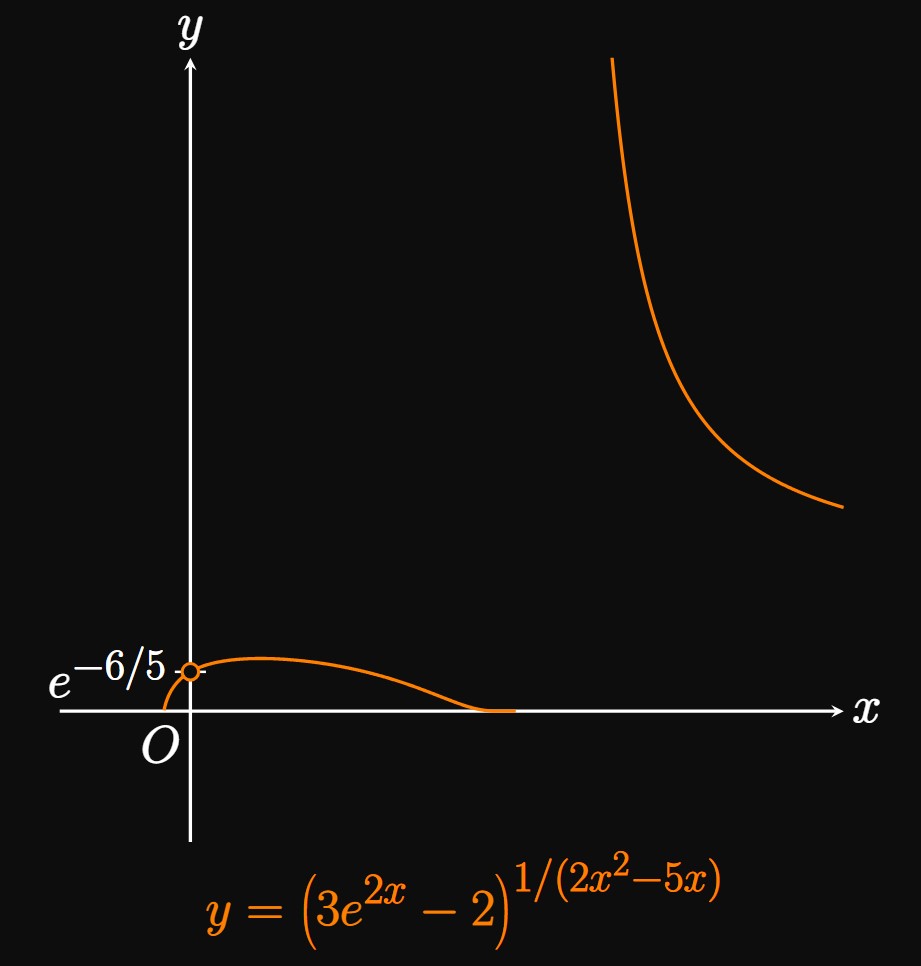
As \(x \to 0^-,\) \[\par{3e^{2x} - 2} \to 1 \and \frac{1}{2x^2 - 5x} \to \infty \pd\] This limit is therefore in the indeterminate form \(1^\infty.\) We first let \[y = \par{3e^{2x} - 2}^{1/({2x^2 - 5x})} \pd \] Taking the natural logarithm of both sides, we get \[ \ba \ln y &= \ln \left[ \left( 3e^{2x} - 2 \right)^{1/({2x^2 - 5x})} \right] \nl &= \frac{1}{2x^2 - 5x} \ln \left( 3e^{2x} - 2 \right) \pd \ea \] Now \[ \ba L &= \lim_{x \to 0^-} \ln y \nl &= \lim_{x \to 0^-} \frac{1}{2x^2 - 5x} \ln \left( 3e^{2x} - 2 \right) \nl &= \lim_{x \to 0^-} \frac{\ln \left( 3e^{2x} - 2 \right)}{2x^2 - 5x} \pd \ea \] This limit is in the indeterminate form \(\indZero,\) so L'Hôpital's Rule gives \[ \ba L &= \lim_{x \to 0^-} \frac{\dfrac{6e^{2x}}{3e^{2x} - 2 \strut}}{4x - 5} \nlLong &= \frac{\dfrac{6 e^0}{3e^0 - 2 \strut}}{4(0) - 5} \nlLong &= -\frac{6}{5} \pd \ea \] Because \(L = -6/5,\) \[\lim_{x \to 0^-} \par{3e^{2x} - 2}^{1/({2x^2 - 5x})} = e^L = \boxed{e^{-6/5}}\] (See Figure 7.)

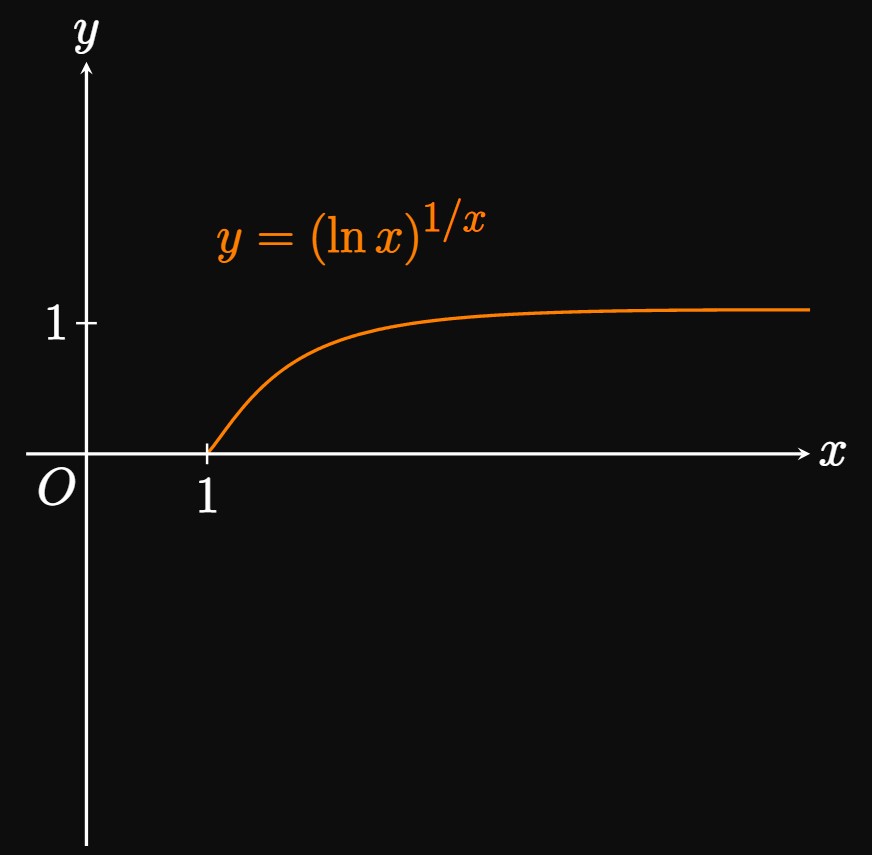
As \(x \to \infty,\) \[\ln x \to \infty \and \frac{1}{x} \to 0 \cma\] so the limit is in the indeterminate form \(\infty^0.\) We first let \[y = \left(\ln x \right)^{1/x} \pd \] Taking the natural logarithm of both sides produces \[\ln y = \frac{1}{x} \ln \left(\ln x \right) \pd\] Then \[ \ba L &= \lim_{x \to \infty} \ln y \nl &= \lim_{x \to \infty} \frac{1}{x} \ln \left(\ln x \right) \nl &= \lim_{x \to \infty} \frac{\ln(\ln x)}{x} \pd \ea \] This limit is in the indeterminate form \(\indInfty,\) so applying L'Hôpital's Rule gives \[ \ba L &= \lim_{x \to \infty} \frac{\dfrac{1}{x\ln x \strut}}{1} \nl &= 0 \pd \ea \] Since \(L = 0,\) we have \[\lim_{x \to \infty} (\ln x)^{1/x} = e^L = e^0 = \boxed{1} \] As shown in Figure 8, the graph of \(y = (\ln x)^{1/x}\) has a horizontal asymptote of \(y = 1.\)