1.5: Formal Definition of a Limit

In Section 1.1 we introduced a working definition of a limit. Using this concept, we explored limit laws and calculated limits algebraically in Section 1.2. But we have yet to define limits formally, through mathematical notation. In this section we learn to build proofs of limit statements, through the following topics:

• Formal Definition of a Limit
• Formal Definitions of One-Sided Limits
• Formal Definitions of Infinite Limits

Formal Definition of a Limit

In Section 1.1 we defined the notation \(\lim_{x \to a} f(x) = L\) as follows: We can make \(f(x)\) arbitrarily close to \(L\) by making \(x\) sufficiently close to \(a\) (but not equal to \(a\)). But how do we express this concept more precisely? Let's introduce a positive number \(\varepsilon\) as a measure of how far \(f(x)\) is from \(L.\) If we want \(f(x)\) to differ from \(L\) by less than \(\varepsilon,\) then we need to determine the values of \(x\) that allow this accuracy. Mathematically, \(\lim_{x \to a} f(x) = L\) means that, for every number \(\varepsilon \gt 0,\) there exists a number \(\delta \gt 0\) such that \begin{equation} \abs{f(x) - L} \lt \varepsilon \if 0 \lt \abs{x - a} \lt \delta \pd \label{eq:del-ep} \end{equation} The quantity \(\abs{f(x) - L}\) is the distance from \(f(x)\) to \(L.\) It must therefore be less than \(\varepsilon\) when \(x\) differs from \(a\) by less than \(\delta,\) that is, when \(\abs{x - a} \lt \delta.\) But we cannot have \(x = a,\) so we impose the condition \(0 \lt \abs{x - a} \lt \delta.\) Geometrically, for \(x\) in the interval \((a - \delta,\) \(a + \delta),\) the curve \(y = f(x)\) lies between the lines \(y = L - \varepsilon\) and \(y = L + \varepsilon.\) We have the freedom to make \(\varepsilon\)—the error tolerance—as small as we wish. Comparing Figure 1A to Figure 1B, we see that if we choose a smaller \(\varepsilon,\) then we may need a smaller \(\delta.\) In words, a smaller error tolerance requires us to make \(x\) closer to \(a\) (without being equal to \(a\)). In proving a limit statement, we must show that \(\eqref{eq:del-ep}\) is true by finding a suitable \(\delta\) for any \(\varepsilon \gt 0.\)

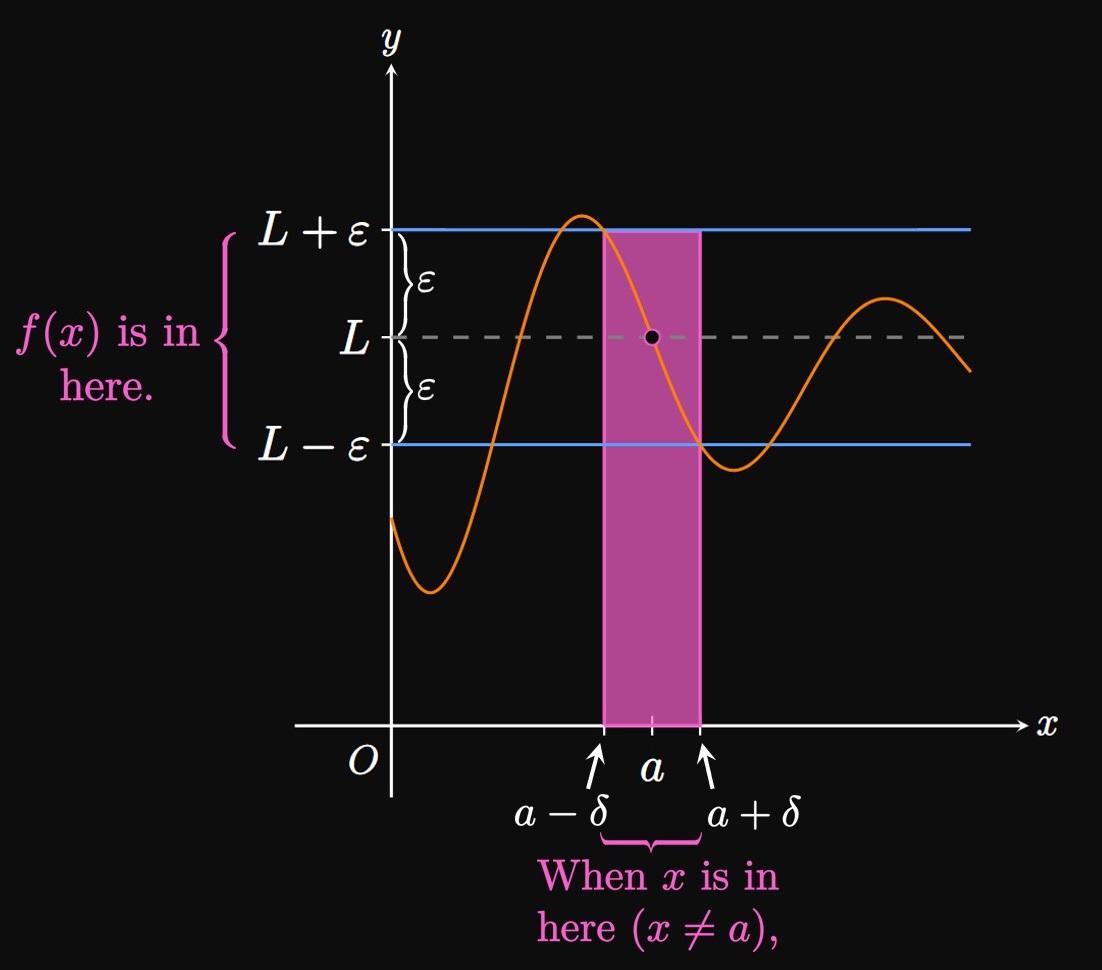
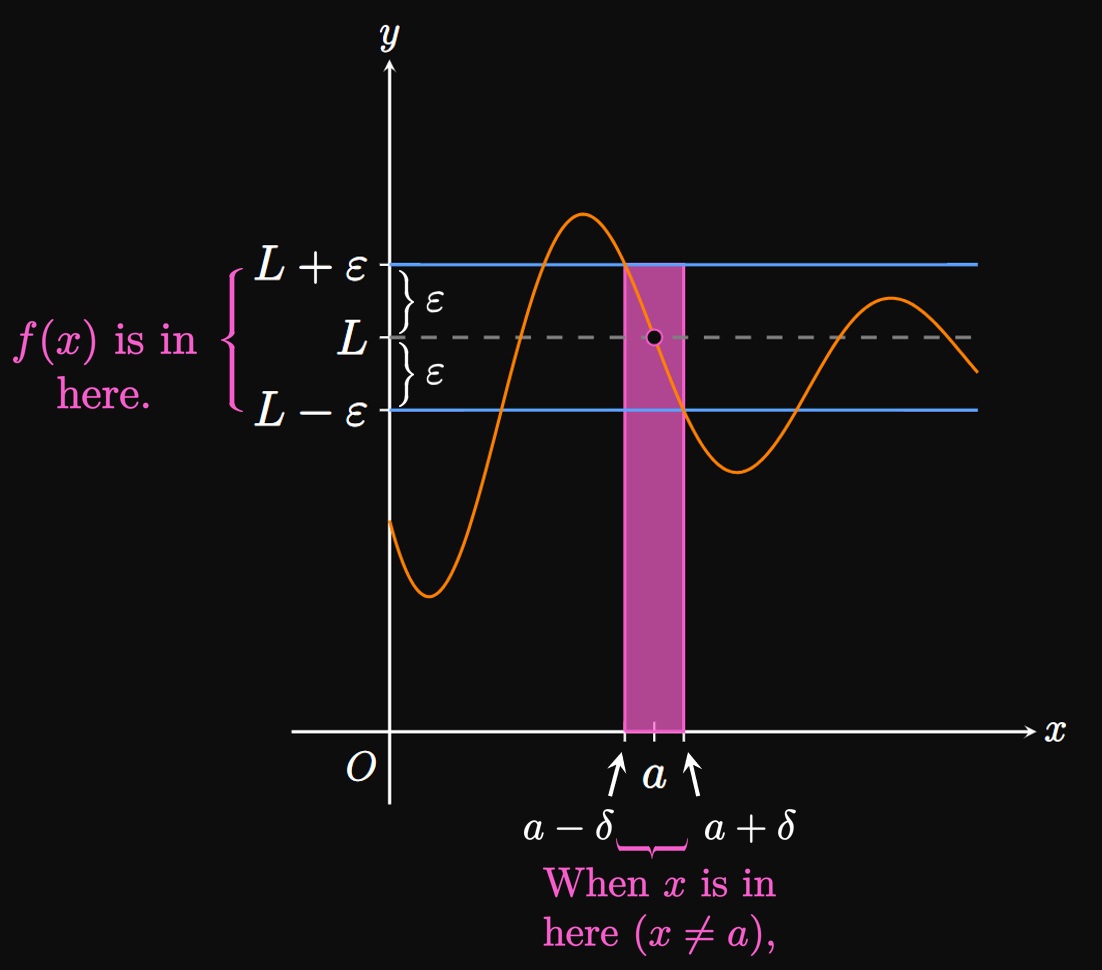
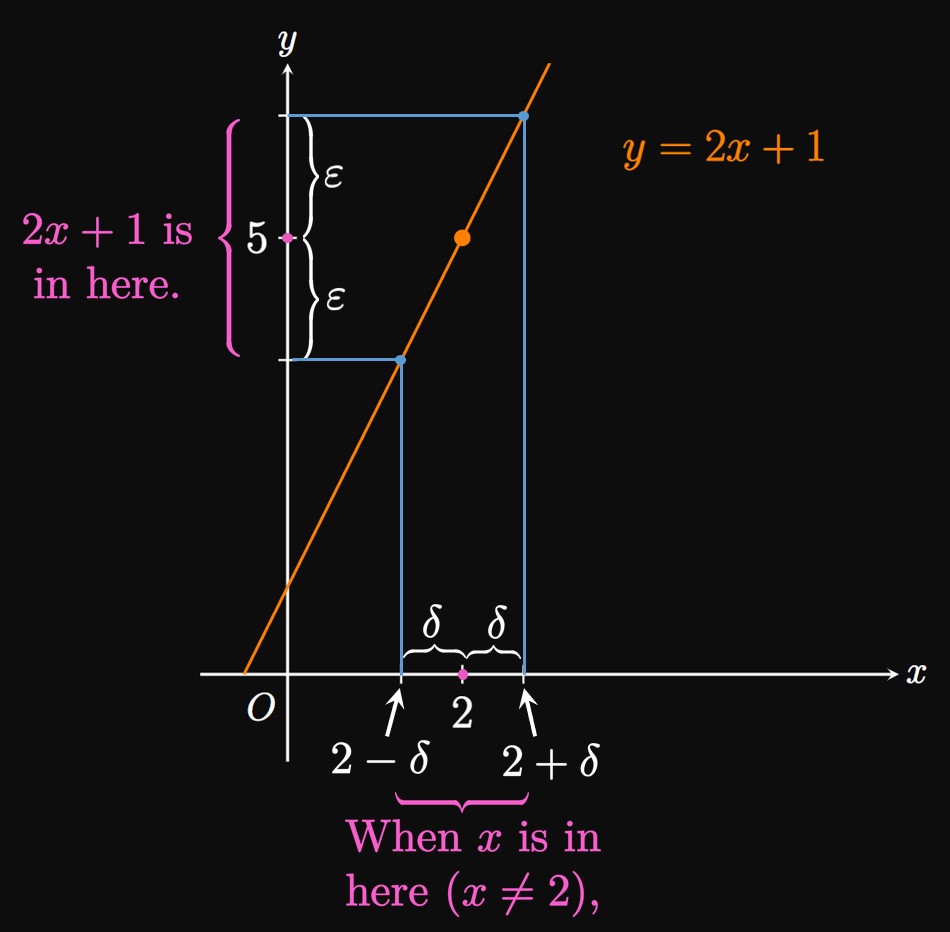
For example, the statement \(\lim_{x \to 2} (2x + 1) = 5\) means, for any \(\varepsilon \gt 0,\) a number \(\delta \gt 0\) exists such that \begin{equation} \abs{(2x + 1) - 5} \lt \varepsilon \if 0 \lt \abs{x - 2} \lt \delta \pd \label{eq:del-ep-ex} \end{equation} To prove this limit, our goal is to express \(\delta\) in terms of \(\varepsilon.\) Think of \(\varepsilon\) as the error tolerance—the number such that \(2x + 1\) differs from \(5\) by less than \(\varepsilon.\) In \(\eqref{eq:del-ep-ex}\) the first inequality becomes \(\abs{2x - 4} \lt \varepsilon,\) or \(\abs{x - 2} \lt \varepsilon/2.\) Comparing this inequality to \(\abs{x - 2} \lt \delta,\) we choose \(\delta = \varepsilon/2.\) Thus, \(\lim_{x \to 2} (2x + 1) = 5\) is true because \[\abs{(2x + 1) - 5} \lt \varepsilon \if 0 \lt \abs{x - 2} \lt \frac{\varepsilon}{2} \pd\] In words, to ensure that \(2x + 1\) is within \(\varepsilon\) of \(5,\) we must make \(x\) less than a distance \(\varepsilon/2\) away from \(2.\) (See Figure 2.) In this form, we have the freedom to choose how close \(2x + 1\) is to \(5\) by requiring a sufficiently small \(\varepsilon.\) For example, if we want \(2x + 1\) to differ from \(5\) by less than \(\varepsilon = 0.05,\) then we need \[\abs{x - 2} \lt \frac{0.05}{2} = 0.025 \iffArrow 1.975 \lt x \lt 2.025 \pd\] Likewise, if \(2x + 1\) is less than \(\varepsilon = 0.01\) away from \(5,\) then we require \[\abs{x - 2} \lt \frac{0.01}{2} = 0.005 \iffArrow 1.995 \lt x \lt 2.005 \pd\] Observe that the interval of allowable \(x\) shrinks as we demand a smaller error tolerance \(\varepsilon.\) This pattern repeats: We have the liberty of making \(2x + 1\) as close to \(5\) as we wish by selecting an arbitrarily small value of \(\varepsilon\) and demanding that \(x\) differ from \(2\) (with \(x \ne 2\)) by no more than \(\varepsilon/2.\) Hence, \(\lim_{x \to 2} (2x + 1) = 5\) is justified. Let's now list a general series of steps to prove a limit statement.

In proving a limit, we first guess an appropriate \(\delta\) and then show that the choice of \(\delta\) satisfies \(\eqref{eq:del-ep}.\) Doing so, we write the proof after we use algebra to decide a suitable \(\delta.\) In mathematics, it is generally easy to check whether a solution is valid—the difficult part is first obtaining the solution. Thus, through clever algebraic tricks, mathematicians often work backward to prove a result.

It may be difficult to prove a limit \(\lim_{x \to a} f(x) = L\) by finding a suitable choice of \(\delta.\) When this occurs, we must compromise. For example, we can determine an appropriate choice of \(\delta\) by considering a simpler problem—for example, by bounding \(\abs{x - a}\) using a larger number, as in Example 2.

Formal Definitions of One-Sided Limits

In the Formal Definition of a Limit, \(\lim_{x \to a} f(x) = L\) is true only if \(x\) differs from \(a\) by less than \(\delta \gt 0\) in either direction of \(a.\) Yet for a one-sided limit, we require \(x\) to differ from \(a\) by less than \(\delta\) in only one direction. We therefore attain the following formal definitions for one-sided limits.

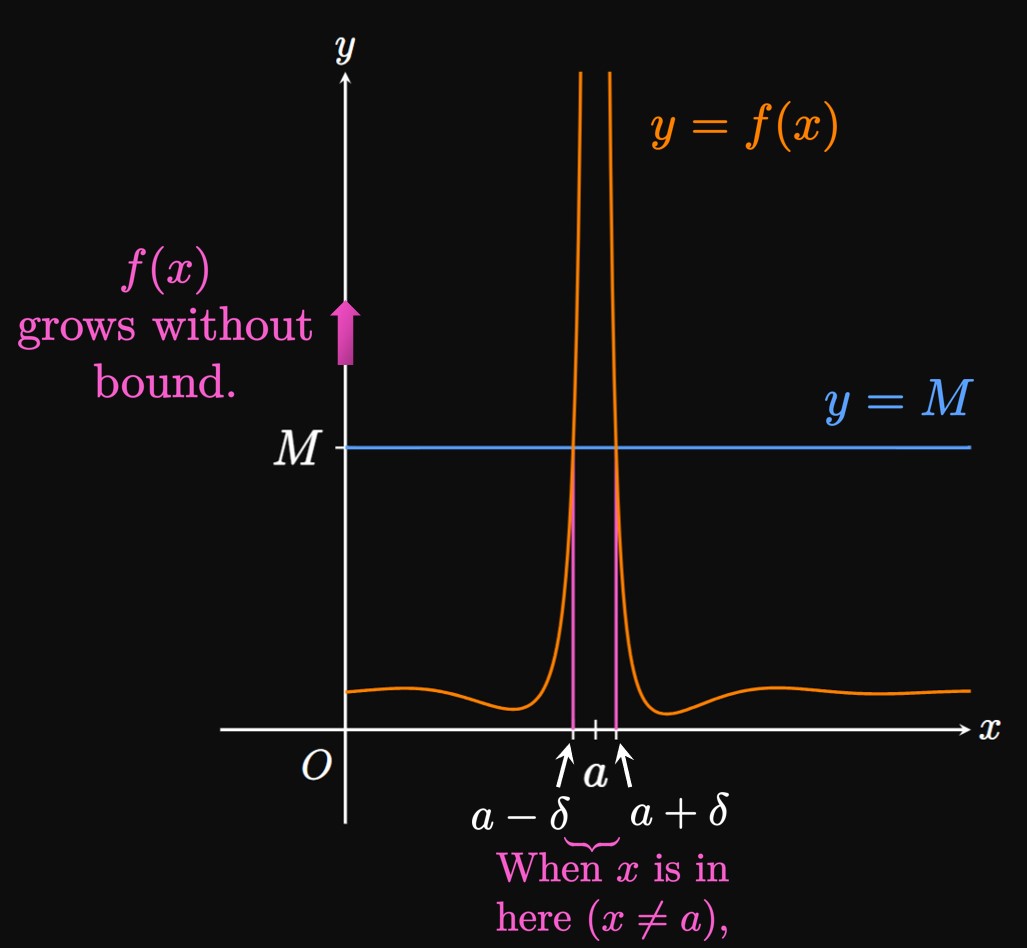
Formal Definitions of Infinite Limits

In Section 1.1 we stated that \(\lim_{x \to a} f(x) = \infty\) means that \(f(x)\) grows without bound as \(x\) is made close to \(a.\) To provide a precise definition, we introduce a positive number \(M\) that bounds \(f(x)\) from below. Given any \(M \gt 0,\) there exists a \(\delta \gt 0\) such that \begin{equation} f(x) \gt M \if 0 \lt \abs{x - a} \lt \delta \pd \label{eq:def-inf-lim} \end{equation} Geometrically, when \(x\) is in the interval \((a - \delta,\) \(a + \delta),\) the curve \(f(x)\) is constantly above the line \(y = M.\) Think of \(M\) as the floor—we can select \(M\) to be any number; the curve \(f\) will remain above \(y = M,\) provided \(x\) differs from \(a\) by less than \(\delta\) (but \(x \ne a\)). (See Figure 3.) Larger values of \(M\) may require smaller values of \(\delta.\)

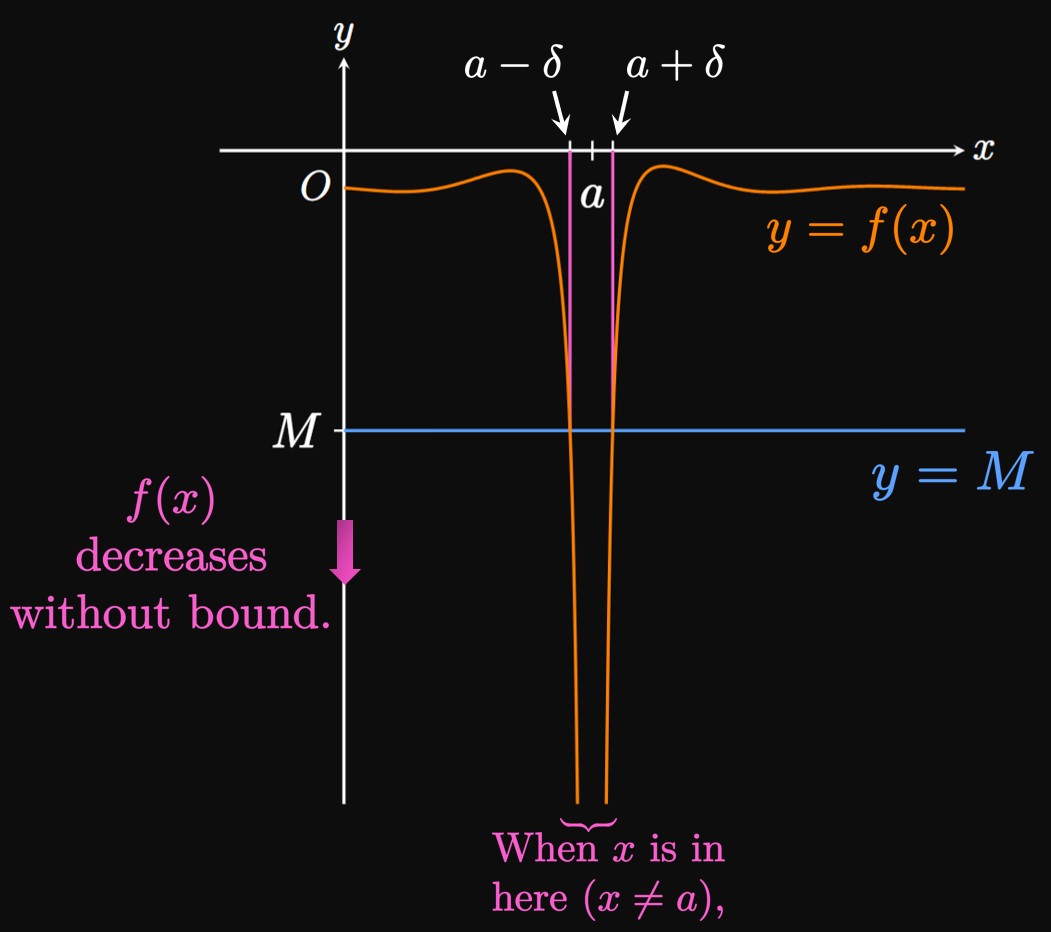
Similarly, the statement \(\lim_{x \to a} f(x) = -\infty\) means that \(f\) decreases without bound as \(x\) is made closer to \(a\) (but \(x \ne a\)). Formally, this limit statement means, for any given negative \(M,\) a number \(\delta \gt 0\) exists for which \begin{equation} f(x) \lt M \if 0 \lt \abs{x - a} \lt \delta \pd \label{eq:def-inf-lim-neg} \end{equation} The number \(M\) is an upper bound for the curve \(f.\) Geometrically, \(y = f(x)\) is below the line \(y = M\) when \(x\) is a distance \(\delta\) away from \(a.\) (See Figure 4.) We can make \(M\) as negative as we wish, provided that we make \(x\) less than a distance \(\delta\) away from \(a\) (but \(x \ne a\)). Think of \(M\) as the ceiling; making \(M\) more negative may require smaller values of \(\delta.\)